






The SOLPENCO tool is based on the MHD model developed by Wu et al. [4] and on the particle code developed by Lario et al. [5]. The scenarios in the synthetic data base comprise a fleet of virtual observers placed at fourteen heliolongitudes and located at either 1.0 AU or 0.4 AU from the Sun. The proton intensities are computed for ten energy channels with mean energies: 0.125, 0.250 0.5, 1, 2, 4, 8, 16, 32 and 64 MeV. The code also provides the integral cumulative fluence profiles above the low-energy bound of each differential channel, although they are labelled using the mean energy of each energy channel. For each scenario, the code also gives the transit time and velocity of the shock from the Sun to the observer, the maximum proton intensity (peak flux), and the total fluence of the SEP event computed from the onset of the event up to the arrival of the associated transient CME-driven shock. For more details about SOLPENCO and its validation we refer the reader to Aran et al. [1], [2], [6] and [3]. SOLPENCO was funded by the ESA contract 14098/99/NL/MM and its validation by the Ministerio de Educación y Ciencia under the project AYA2004-03022.
The SOLar Particle ENgineering COde 2 (SOLPENCO2) tool was developed under the SEPEM Project [7]. It is based on a version of the University of Barcelona’s Shock-and-Particle (SaP) model that was built in collaboration with the KU Leuven [8; see also 9]. During 2015-2016, different aspects of the first version of SOLPENCO2 were improved or updated, under the ESA’s contract SOL2UP (ESA contract No. 4000114116/15/NL/HK). The following description includes these updates.
The SOLPENCO2 tool is an improved version of SOLPENCO in the sense that it significantly extends the range of heliocentric radial distances and proton energies provided by SOLPENCO. SOLPENCO2 furnishes the SEPEM/SAT (Statistical Analysis Tools, [7 and 10]) with 5-300 MeV proton peak flux and event fluence heliocentric radial power-law dependences, derived from the modelling of ten reference gradual proton events. The complexity of the SOLPENCO2 tool prevents the handling of it by a non-expert user; and thus, it is not possible to directly use it in this server.
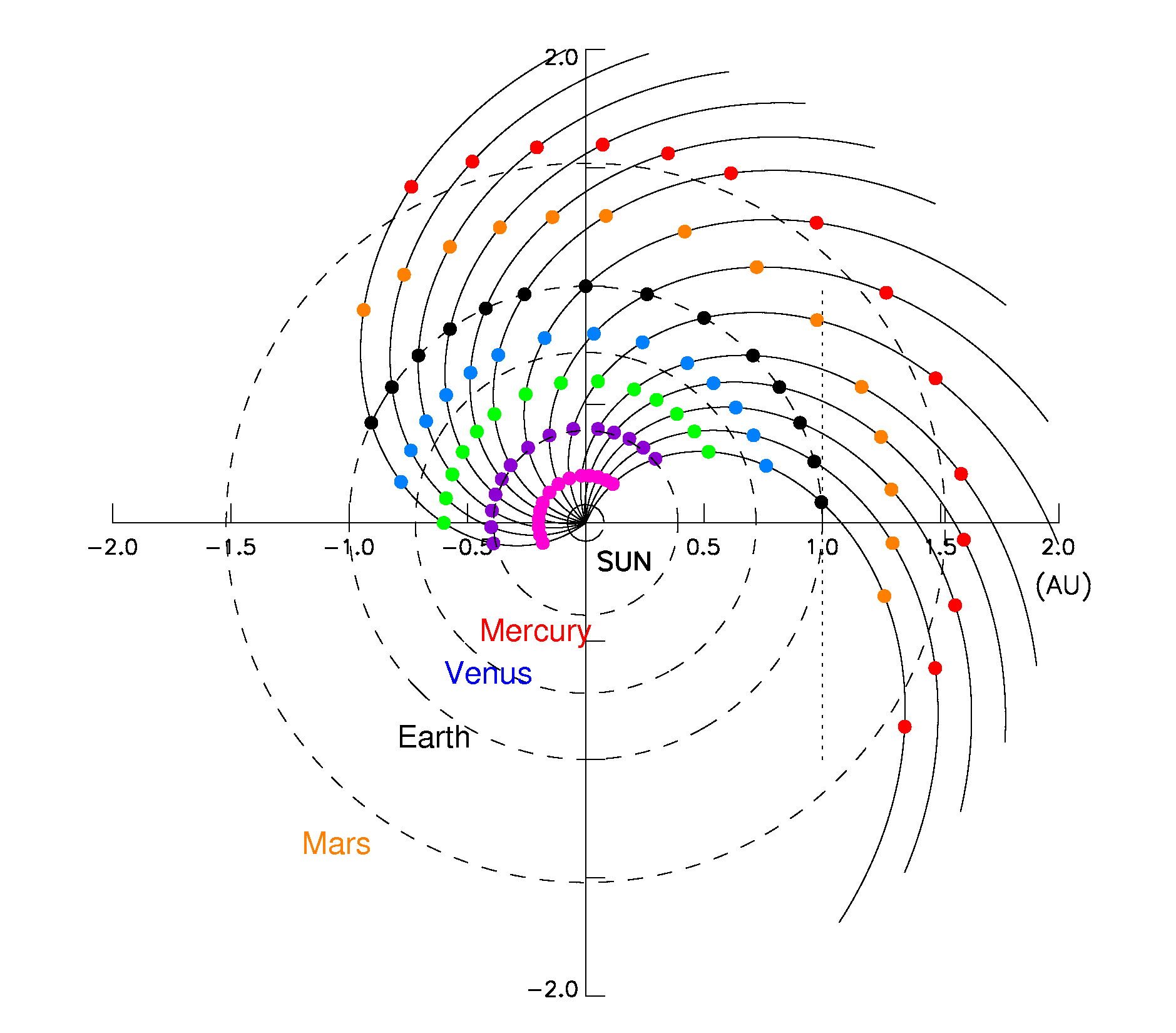
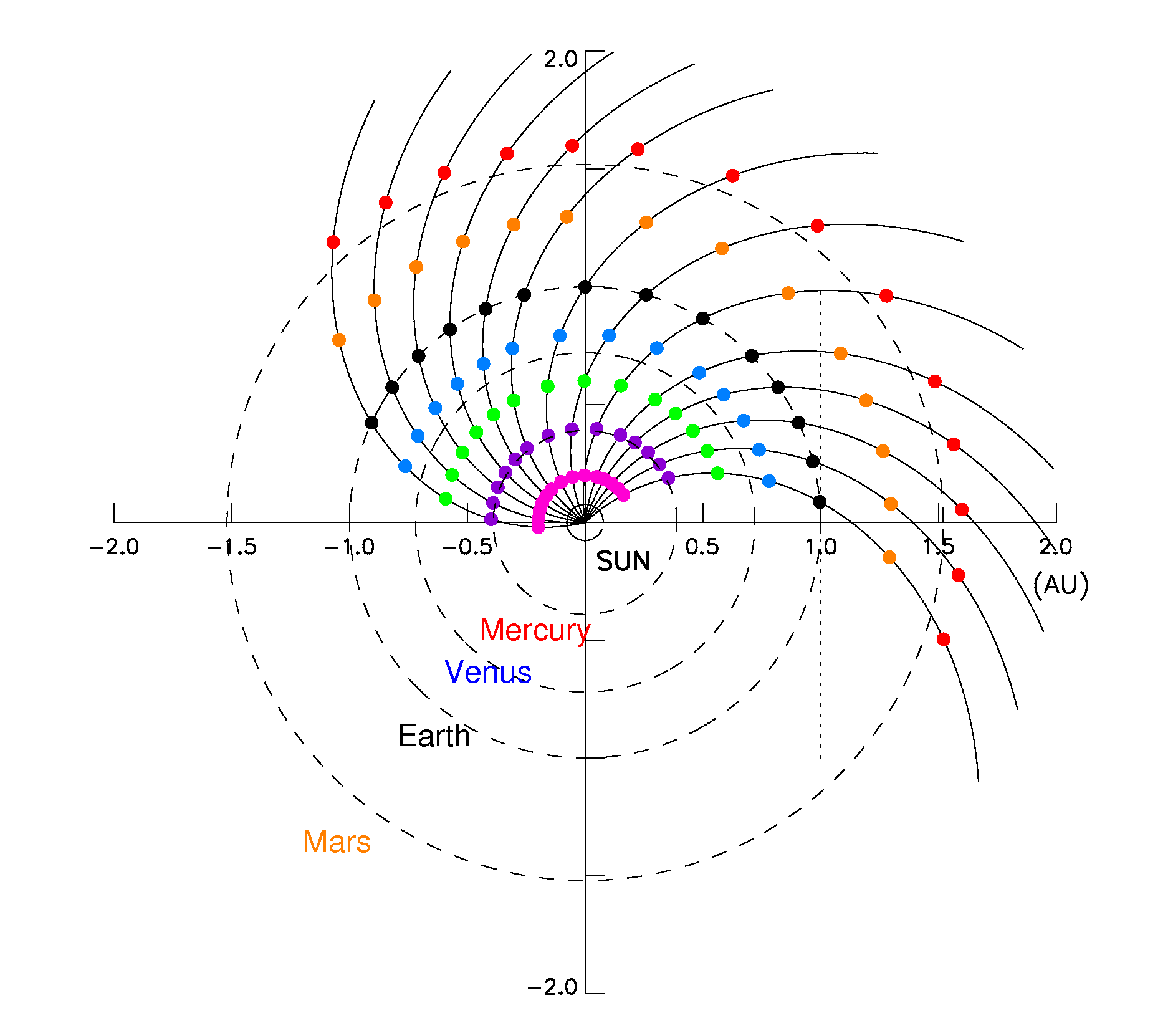
The 249 out of the 263 SEP events events observed at 1 AU between January 1988 and March 2013, contained in the SEPEM Reference Event list (REL), are classified into one of the ten event categories and the corresponding radial scales are applied. This subset of REL is hereafter named as the SEPEM Radial-dependent Reference proton Event List (SREL). In this way, the event list at 1 AU is replicated at seven heliocentric radial distances between 0.2 AU (approximately, half the mean distance of Mercury to the Sun) and 1.6 AU (Mars orbit); thus, allowing the inclusion of interplanetary missions in the SEPEM/SAT. The output of SOLPENCO2 consists of two files: one containing the scaled-to-observed (1 AU) peak intensity ratios for each of the 249 SEP events and for seven virtual observers located at 0.2, 0.4, 0.6, 0.8, 1.0, 1.3 and 1.6 AU; and the other one containing the corresponding SEP event fluence ratios. As shown in Figure 1, the virtual observers are placed along the same interplanetary magnetic field (IMF) line as the 1 AU-observer (i.e. the Earth’s nominal magnetic field line connecting with the Sun).
SOLPENCO2 is designed for the description of gradual solar proton events, originating from any heliolongitude (the range of values is shown in Figure 1) as seen from virtual observers located within 0.2 AU and 1.6 AU. For any modelled event, the tool provides the proton differential intensity-time profiles for the reference energy channels defined in SEPEM (from 5 MeV to 200 MeV, [7]) plus a higher energy channel up to 300 MeV [11].

|

|
| Figure 1. Location of the observers for the slow (left) and the fast (right) wind regimes simulated. | |
The SEP intensity profiles depend on how the magnetic connection of the spacecraft (the observer) is established with the particle source, on how efficiently protons are accelerated and injected by the shock into the connecting magnetic flux tube(s), and on how the IMF irregularities modulate this population during its journey in space [12]. To generate the SOLPENCO2 synthetic SEP events, a new MHD model was developed for the simulation of the CME-driven shocks from near Sun to Mars orbit [8 and13]. The shock propagation model provides values of the MHD variables at the point of the shock front that magnetically connected to the observer (or cobpoint) [14 and 15]; these values are used as inputs to a particle transport model [5]. These models allow computing the injection rate of shock-accelerated particles at a given time, Q, which is a source term in the transport equation describing the propagation of protons along the IMF, towards the observer.
Figure 1 depicts the longitudinal extension covered by SOLPENCO2 for each radial position of the observer. SOLPENCO2 includes simulations of the interplanetary shock propagation on top of two different solar wind regimes, with a speed of 365 km/s, at 1 AU, for the slow case (left panel of Figure 1) and with a speed of 595 km/s for the fast case (right panel of Figure 1).
For instance, the solar source longitudinal span covered by the simulations provided in SOLPENCO2 at 1 AU extends from W85 to E65. In this range 14 different observers (or solar source sites) are considered: W85, W75, W65, W55, W45, W30, W15, W00, E15, E25, E35, E45, E55 and E65.
For each kind of solar wind regime, SOLPENCO2 includes 8 different shock simulations characterised by different times of the shock arrival to 1 AU: from 17 to 48 hours on top of the fast wind and from 24 to 67 hours on top of the slow wind. Also, to try to cover a larger number of possible scenarios than in SOLPENCO, the shock simulations are performed for two types of shocks according to their longitudinal extension: narrow and wide shocks. Hence, the shock data base contains the cobpoint for 12,544 scenarios (7 radial distances x 14 heliolongitudes x 4 particle transport conditions x 16 shocks x 2 solar winds). Hence, using this data set, it would be possible to generate large data base of synthetic SEP intensity-time profiles with SOLPENCO2.
Any other intermediate solar-interplanetary scenarios not stored in the SOLPENCO2 data base is derived by interpolation. SOLPENCO2 uses the algorithms developed in SOLPENCO to interpolate among the four pre-calculated gradual SEPs profiles which have the closest angular positions and transit times of the shock (from the Sun to the observer) to the corresponding observed values for a given event. In this way, it is possible to produce within minutes a synthetic SEP event for a given observed event at 1 AU or at non-Earth heliocentric radial distances.
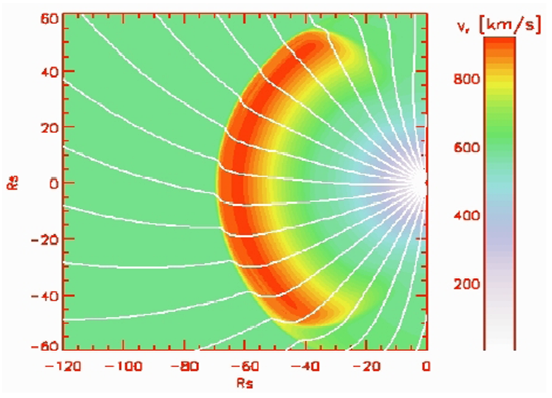 |
| Figure 2. Snapshot of an interplanetary shock simulation propagating from Sun to ~0.5 AU. Solar wind plasma speed is colour coded (as indicated) and a set of IMF lines (white lines) is also shown. |
The strength of the shock is characterised by means of the different plasma values at the cobpoint [15]; namely: the normalised downstream-to-upstream plasma velocity jump, VR; the magnetic downstream to upstream ratio, BR; and the local angle between the upstream IMF and the normal to the shock front, θBn [5 and 15]. As the shocks expands and evolves in space, the cobpoint slides along the front of the shock and hence, the plasma values change with time (as they depend on the local unperturbed upstream and on the shocked downstream solar wind conditions). Figure 3 (from [3]) sketches this concept: particles accelerated at the front of the shock are injected in the magnetic field lines connecting the observer (black diamond) with the shock at the cobpoint (red point); in this particular scenario, the position of the cobpoint moves towards the nose of the shock (red arrow), consequently, the efficiency of the injection of shock-accelerated particles increases. Therefore, the values at the cobpoint, for a given time and a given observer considered in the data base of SOLPENCO2 can be derived.
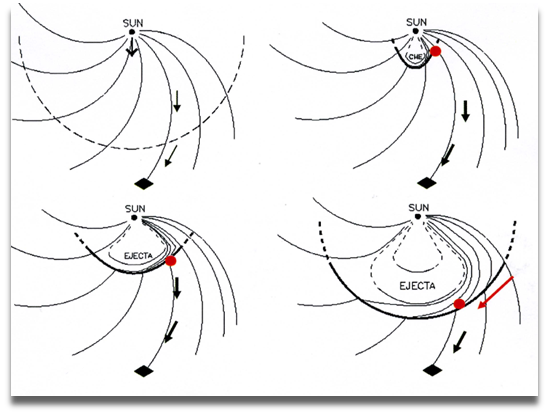 |
| Figure 3. Cartoon showing the evolution of the cobpoint with respect to the front of the CME-driven shock and the position of the observer, for a given solar-interplanetary scenario. |
This injection rate changes with time, as it depends on the existing shock jump conditions at the cobpoint. Q is the source term in the transport equation: it gives the efficiency of the shock as injector of accelerated particles in interplanetary medium. The mean free path, λ, describes the propagation of particles in the diffusive-focused transport model which is the result of the interaction between energetic particles and IMF irregularities in the quasi-linear approximation [18]. For the description of some events, the presence of a turbulent magnetic foreshock region is required to reproduce the flux and the anisotropy values observed in the spiky energetic storm particle (ESP) component at the shock arrival. This foreshock is represented by a region of a given width just ahead of the shock, whose particle mean free path is much smaller than that in the rest of the upstream medium [5]. The transport equation is solved for each shock scenario by using a numerical algorithm that assumes that the inner boundary limit is at the radial distance of the cobpoint, which evolves as the shock propagates [5].
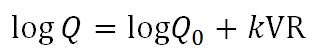
| (1) |
To model the reference events with SOLPENCO2, averaged values for k and Q0 are assumed. Then, the variation of the injection rate for each scenario is computed by using Eq. (1) because the values of VR are derived from the MHD simulation of the corresponding shock.
The main difference between SOLPENCO and SOLPENCO2 lies in the purpose of the two tools. SOLPENCO is a stand-alone tool ready to be operated by any user with some knowledge of SEP events, while SOLPENCO2 is designed for providing inputs to the SEPEM interplanetary statistical analysis model. SOLPENCO2 uses scaling factors that are specific for the reference events, in order to match 1 AU data, whereas SOLPENCO used a universal scaling factor for its SEP events database. Both, however, share the same modular approach, which would enable the possibility of developing another tool more similar to the first SOLPENCO, using the simulations available in SOLPENCO2.
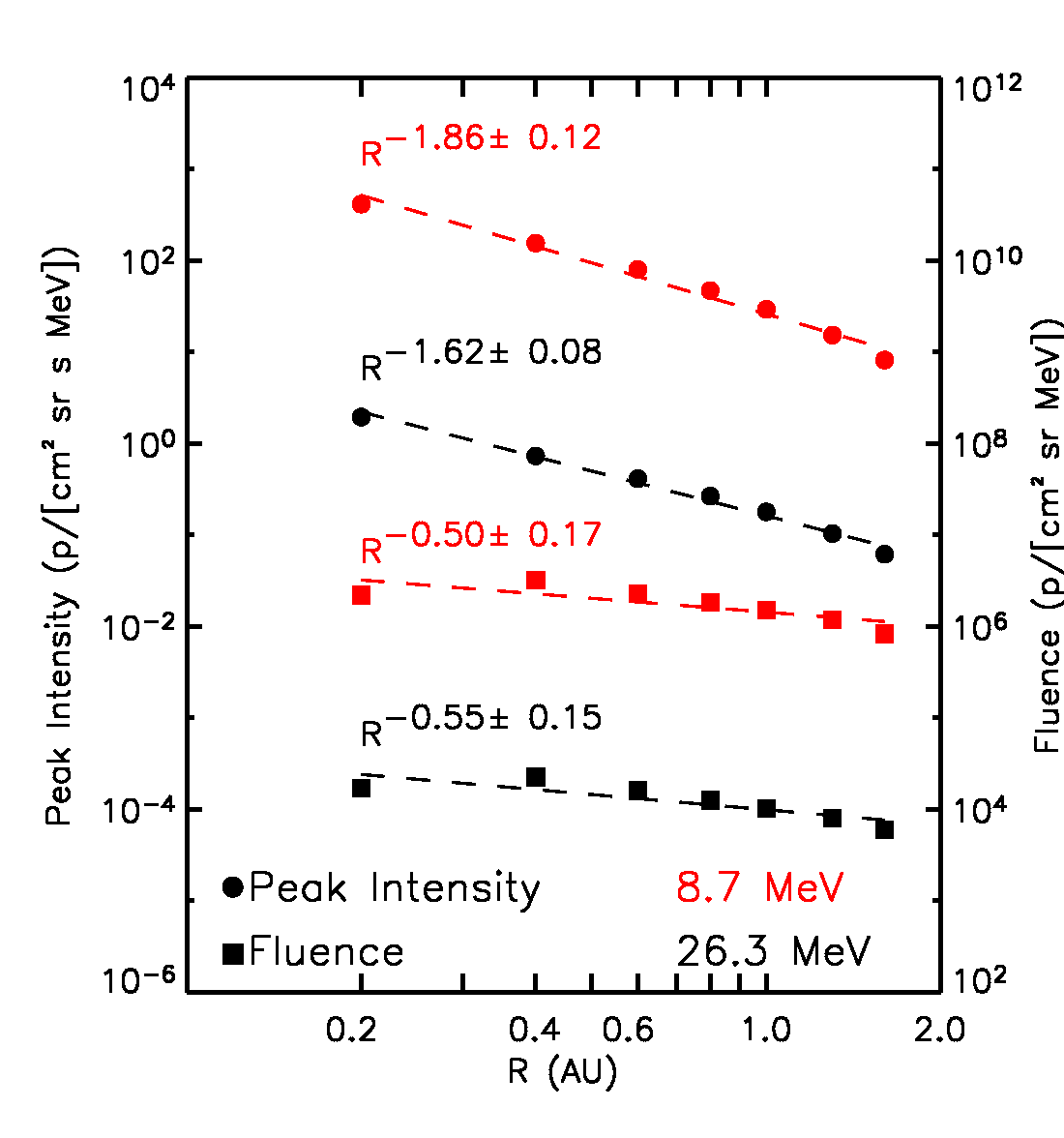 |
| Figure 4. Example of the radial dependences for the peak flux and fluence derived for a specific solar-interplanetary scenario, for two energies. |
The above mentioned physics-based model [8 and 9] was used to derive the radial variation of the peak intensity and fluence for ten SEP event case studies. The SEPEM statistical model is based on 1 AU cleaned data from 1973 to 2016. The solar origin of 249 out of 263 SEP events (compound and isolated) of the SREL (between January 1988 and April 2013) was determined. The intensity and maximum energy attained in the events were also analysed. Then, the SREL events were classified into the ten sub-types in order to assign to them the corresponding radial dependences. This allows to scale peak intensities and fluences to other radial distances and make use of the SEPEM statistical modelling machinery available at 1 AU [7 and 10].
Note that in this section, we refer to an "SEP event" following the scientific definition: a particle enhancement generated by a specific solar activity (either flare or/and CME) and often associated with interplanetary shocks. In the statistical analysis, (both at 1 AU and away from 1 AU), a particle intensity enhancement above a prescribed threshold in the 7.23—10.46 MeV channel is defined as an SEP event. Consequently, an event defined in this latter manner may be compound of different SEP events as per the former definition. In the following, when we refer to compound events, these are particle enhancements consisting of a series of SEP events defined by their solar and interplanetary (if identified) sources.
Two sets of scaling factors were established per event at 1 AU: for peak fluxes and for upstream fluences, between the observed and synthetic values. Consistency between the total fluence simulated at 1 AU and the observed value was checked by calculating the total-to-upstream observed fluence ratios.
Figures 5, 6 and 7 show the comparison of the observed intensity-time profiles for the SEPEM standard differential channels and the synthetic profiles produced by SOLPENCO2 for each SEP event.
|
December 14, 2006 SEP event: 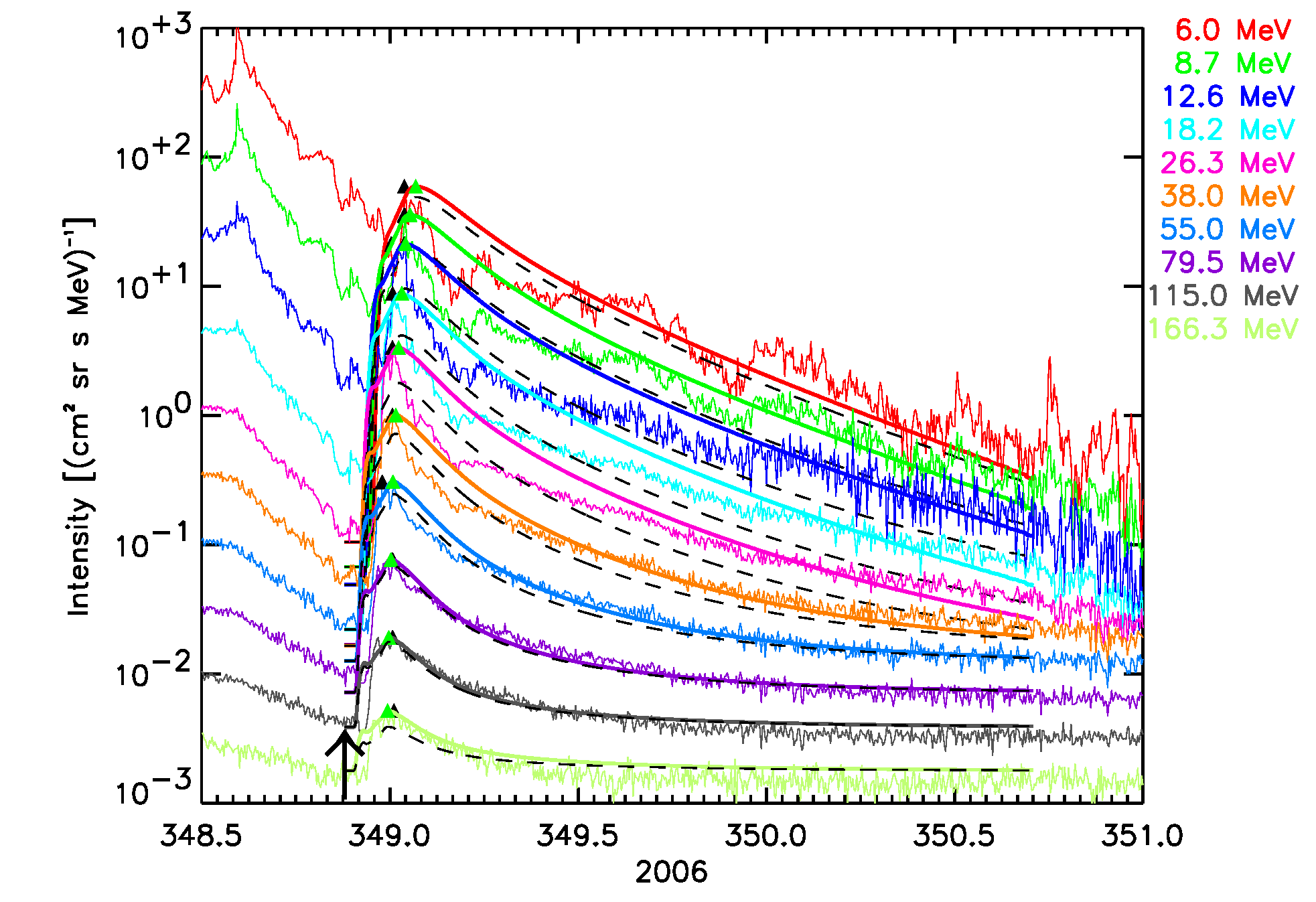 |
June 10, 2000 SEP event: 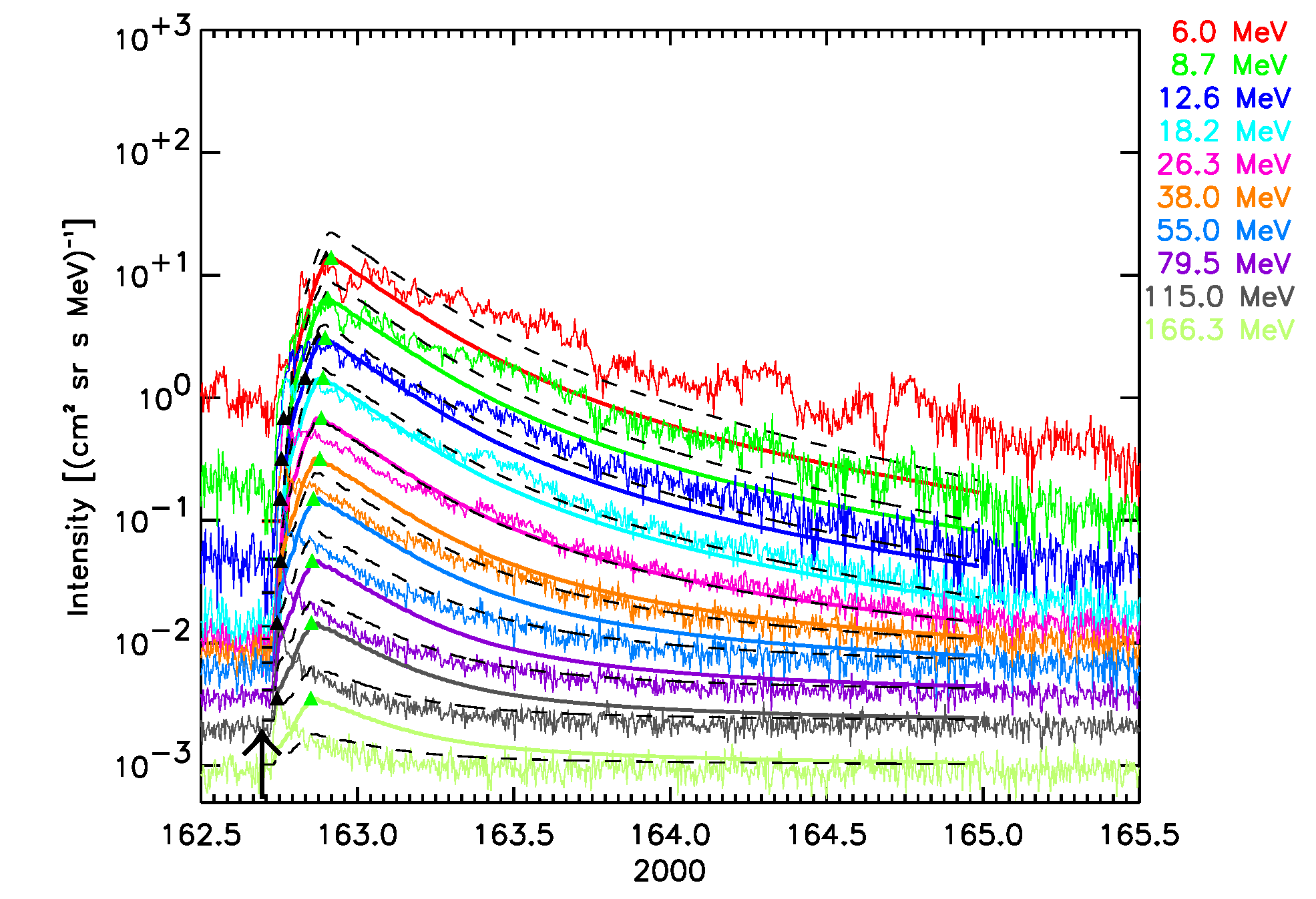 |
April 4, 2000 SEP event: 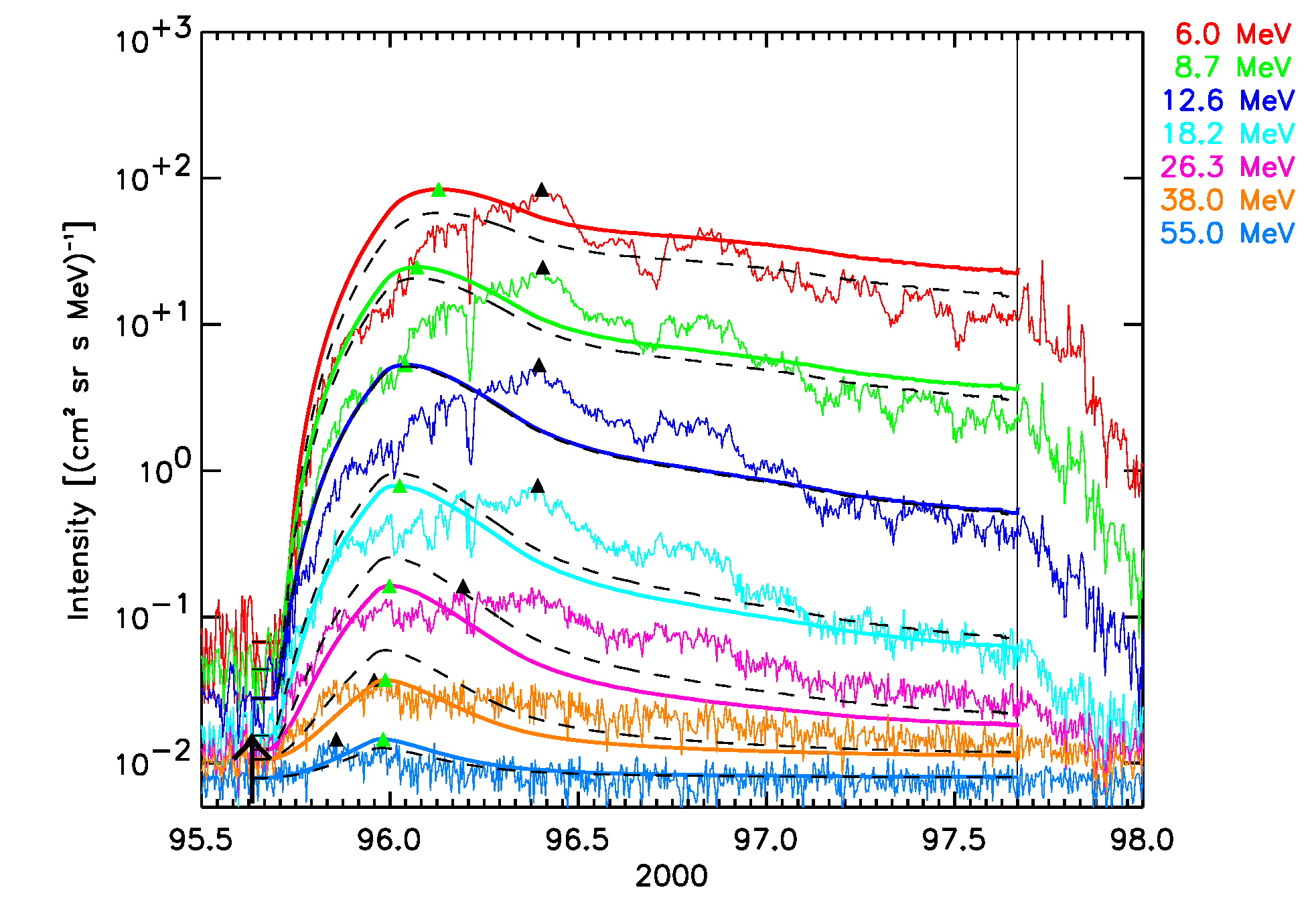 |
|
June 6, 2000 SEP event: 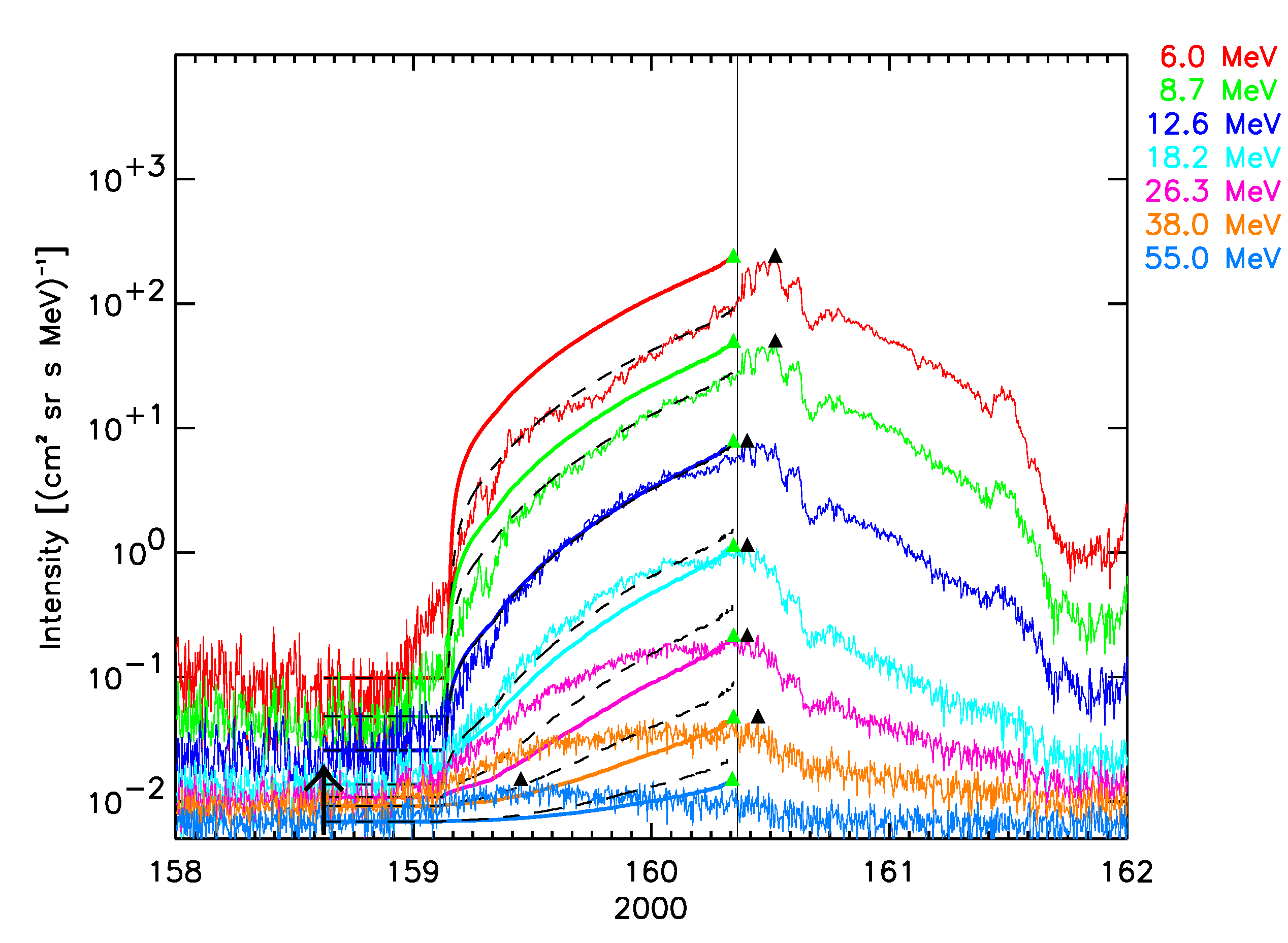 |
March 29, 2001 SEP event: 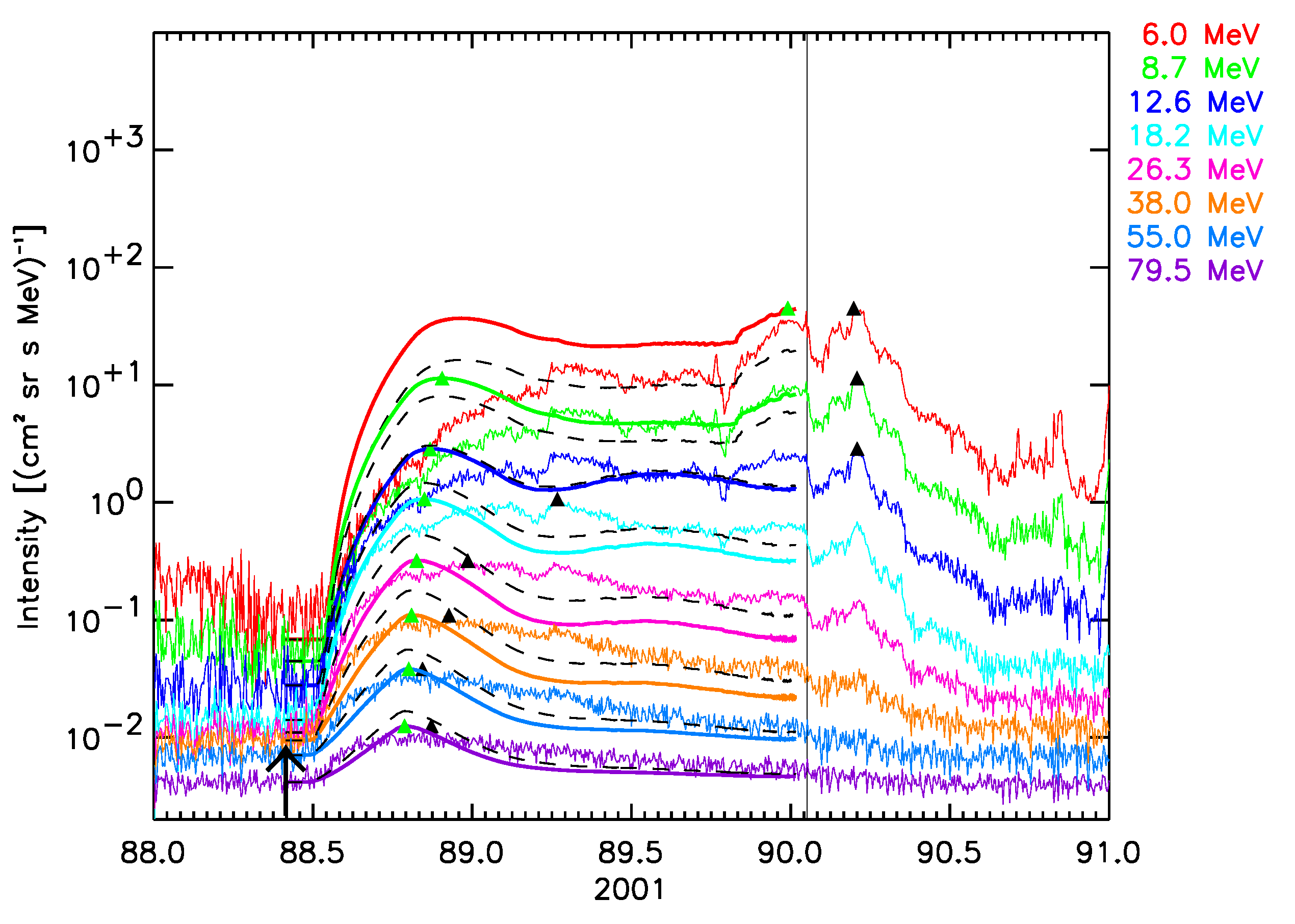 |
December 13, 2006 SEP event: 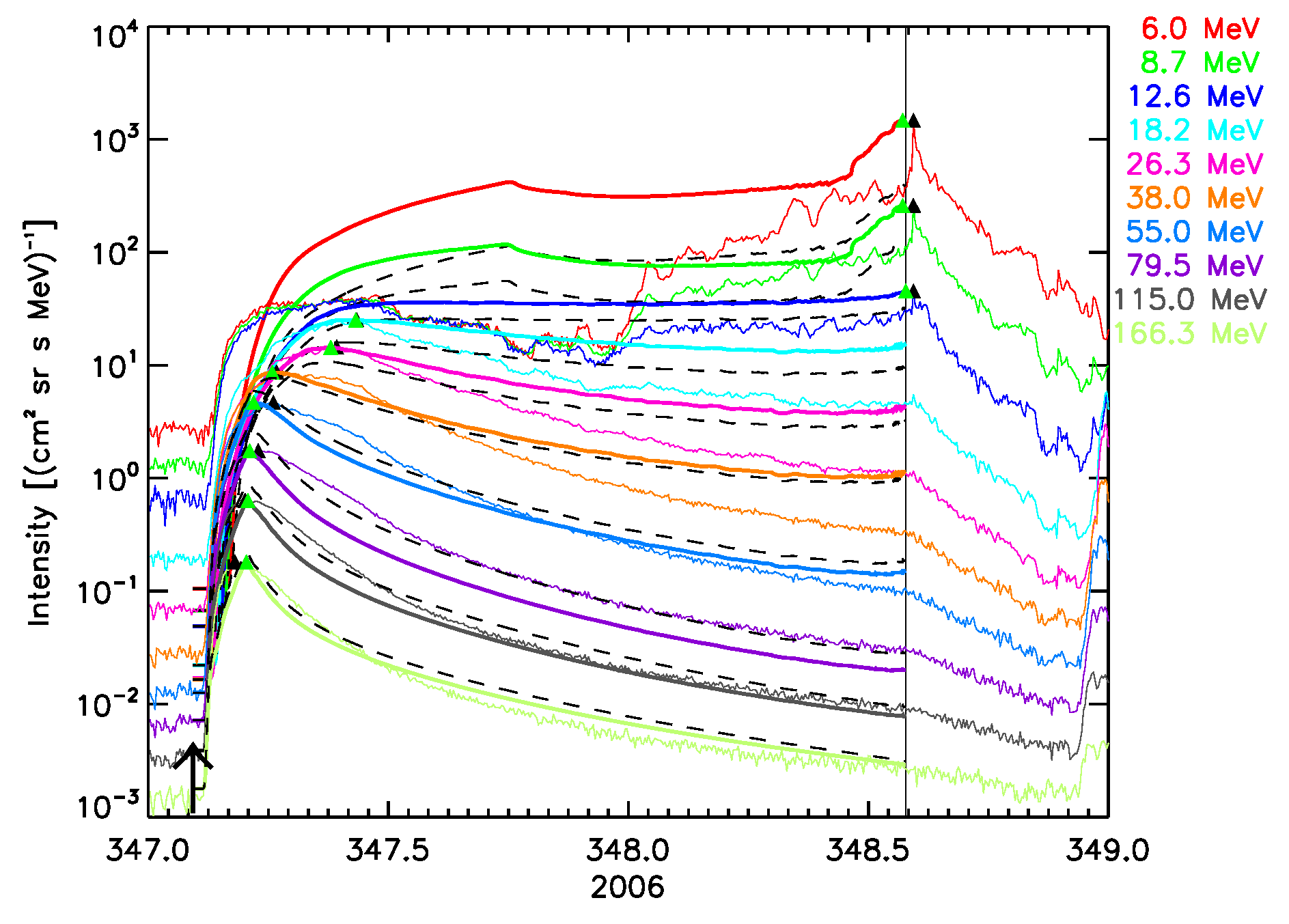 |
Figure 5. The six SEPEM reference cases, comparison with 1 AU Reference data. SOLPENCO2 synthetic flux profiles scaled per channel using: peak intensity (solid lines); upstream fluence (dashed lines). Observed and synthetic intensities are displayed for the mean energy, indicated at the right hand side of each panel (in MeV), of the SEPEM Reference Data energy channels. Peak intensities: observed (black triangles), simulated (green triangles). Vertical lines mark the passage of an interplanetary shock by the ACE spacecraft at L1.
|
March 6, 1989 SEP event: 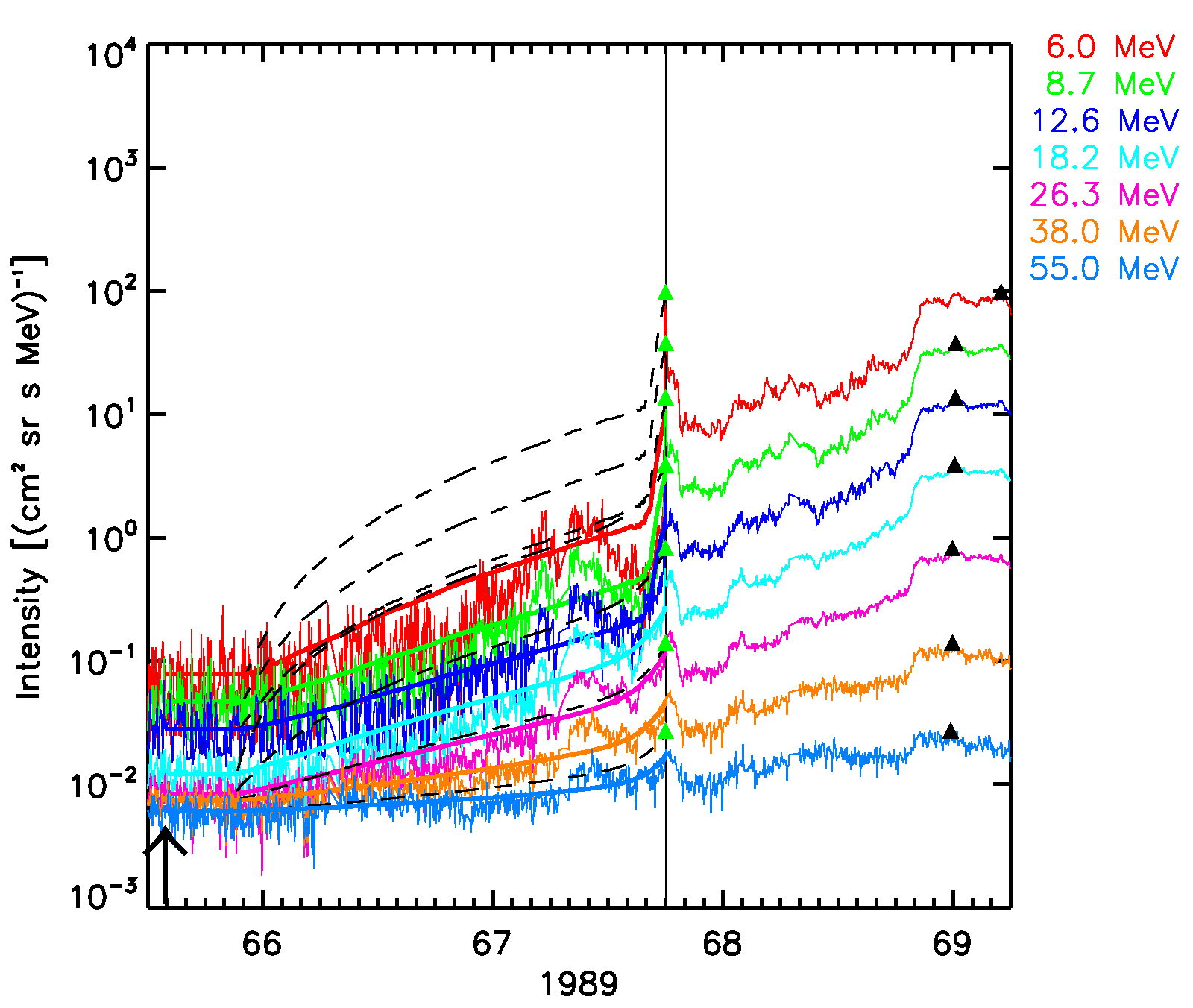 |
September 24, 2001 SEP event: 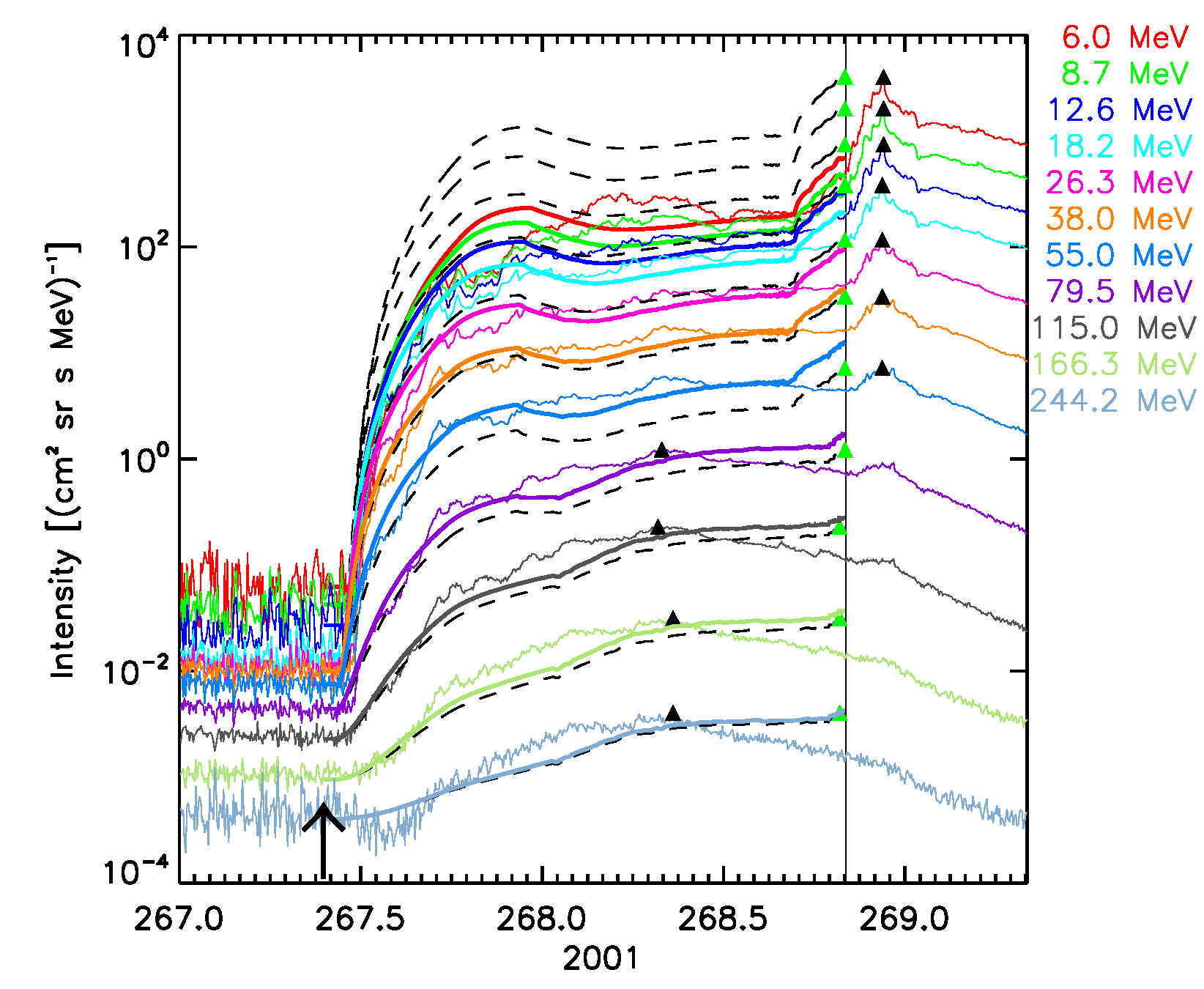 |
|
|
March 13, 2012 SEP event: 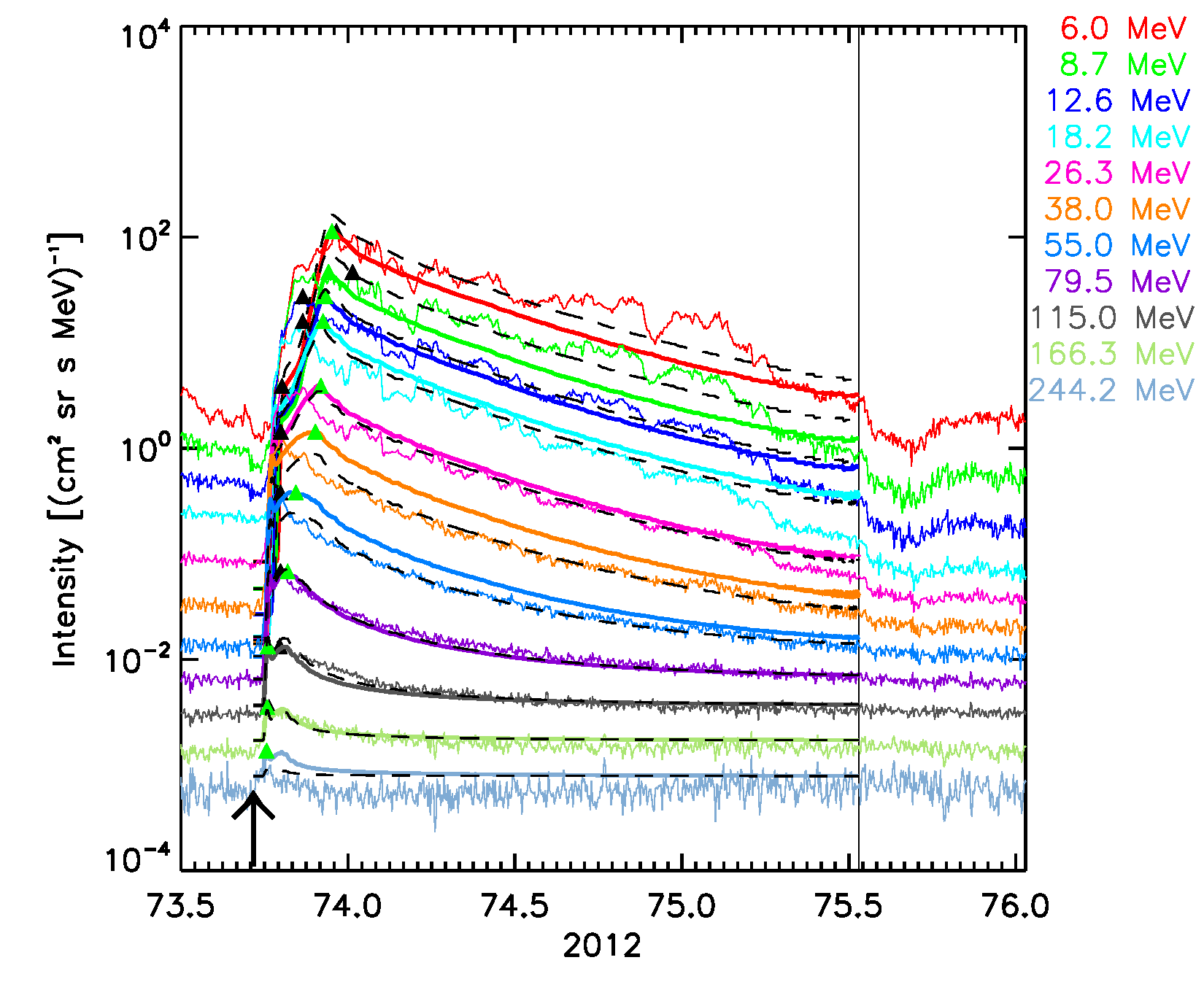 |
October 29, 2003 SEP event: 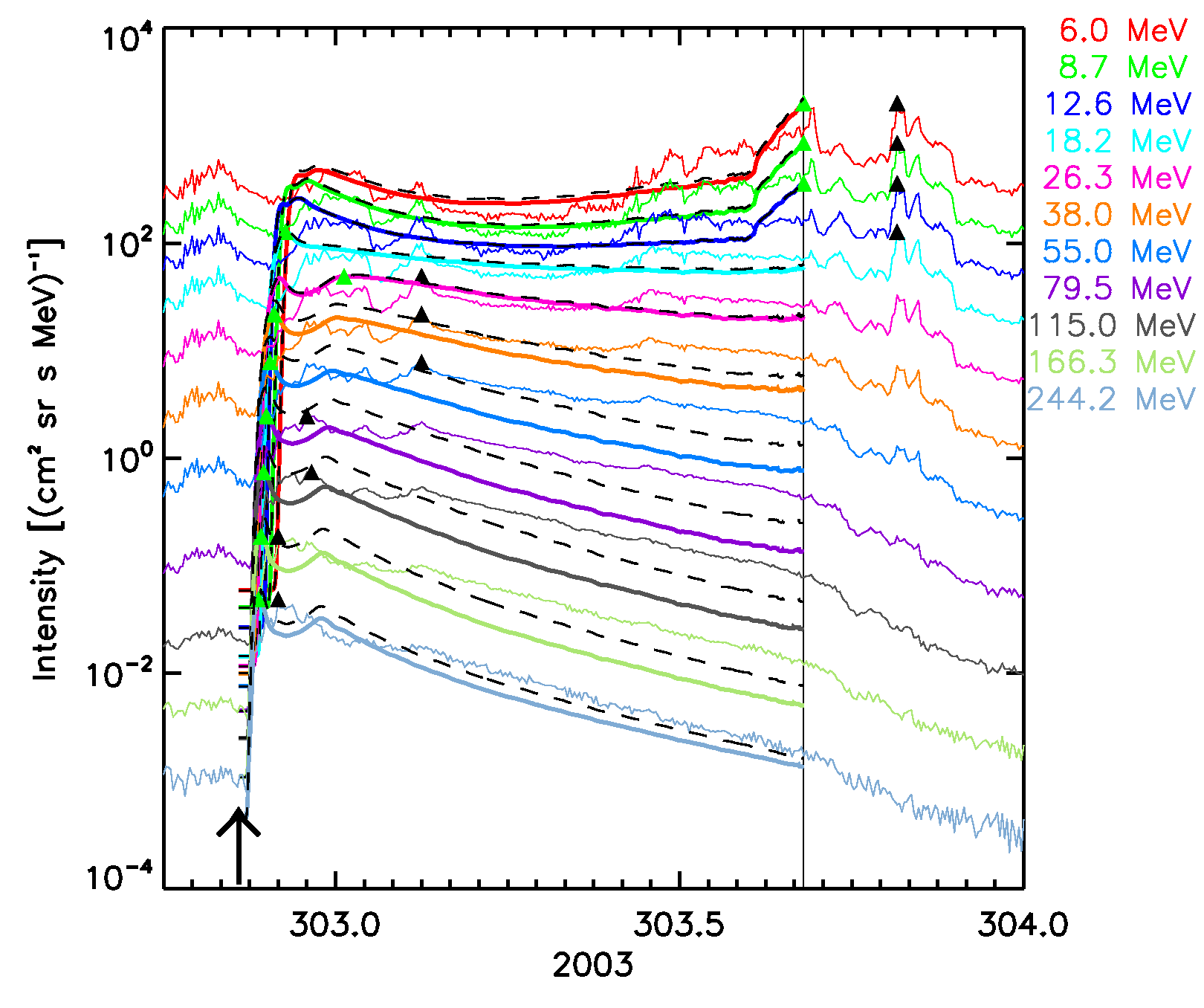 |
For each simulated energy, the synthetic upstream flux profiles generated at 0.2, 0.4, 0.6, 0.8, 1.3 and 1.6 AU are scaled using these two sets of scaling factors. Note that the virtual observers are placed along the same interplanetary magnetic field line as the observer at 1 AU.
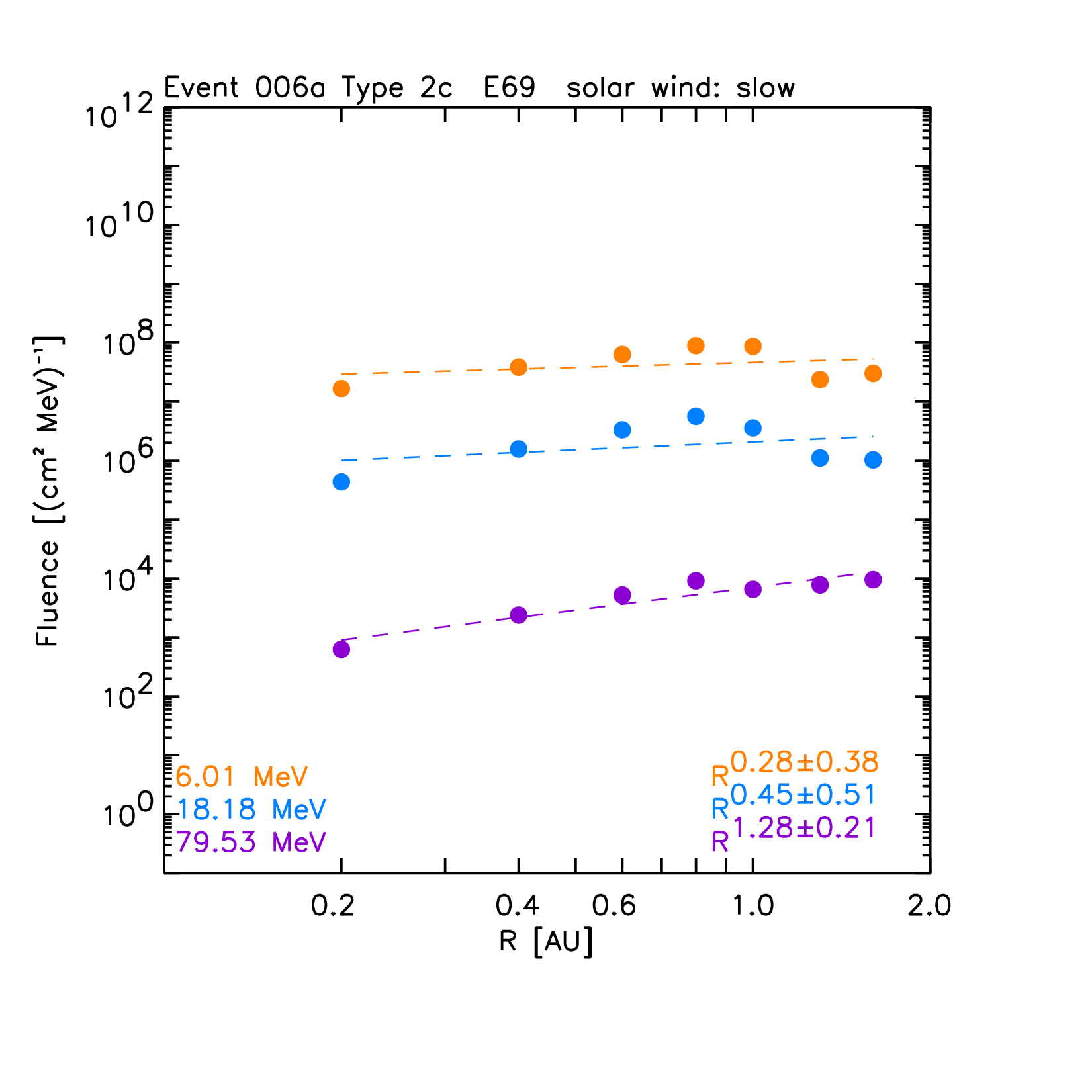
The left panels of Figure 8 show the synthetic intensity-time profiles seen by the virtual observers, for selected proton energies (indicated in each panel) for the ten reference events. The right panels of Figure 8 show the corresponding radial variations for the peak intensity (circles) and fluences (squares). A power law fit of these quantities with the radial distance (dashed lines) and the derived radial index are indicated. Note that the radial variations found for peak intensity and fluence are independent of the scaling factors but a direct result of the physical model.
At this stage, for the calculation of the total fluence of the events (indicated by squares in the right panels of the graphs in Figure 8), we assume that the observed downstream-to-total fluence ratios (DTFRs) keep constant with the radial distance. The final adopted values for the DTFRs are described below.
|
December 14, 2006 SEP event: 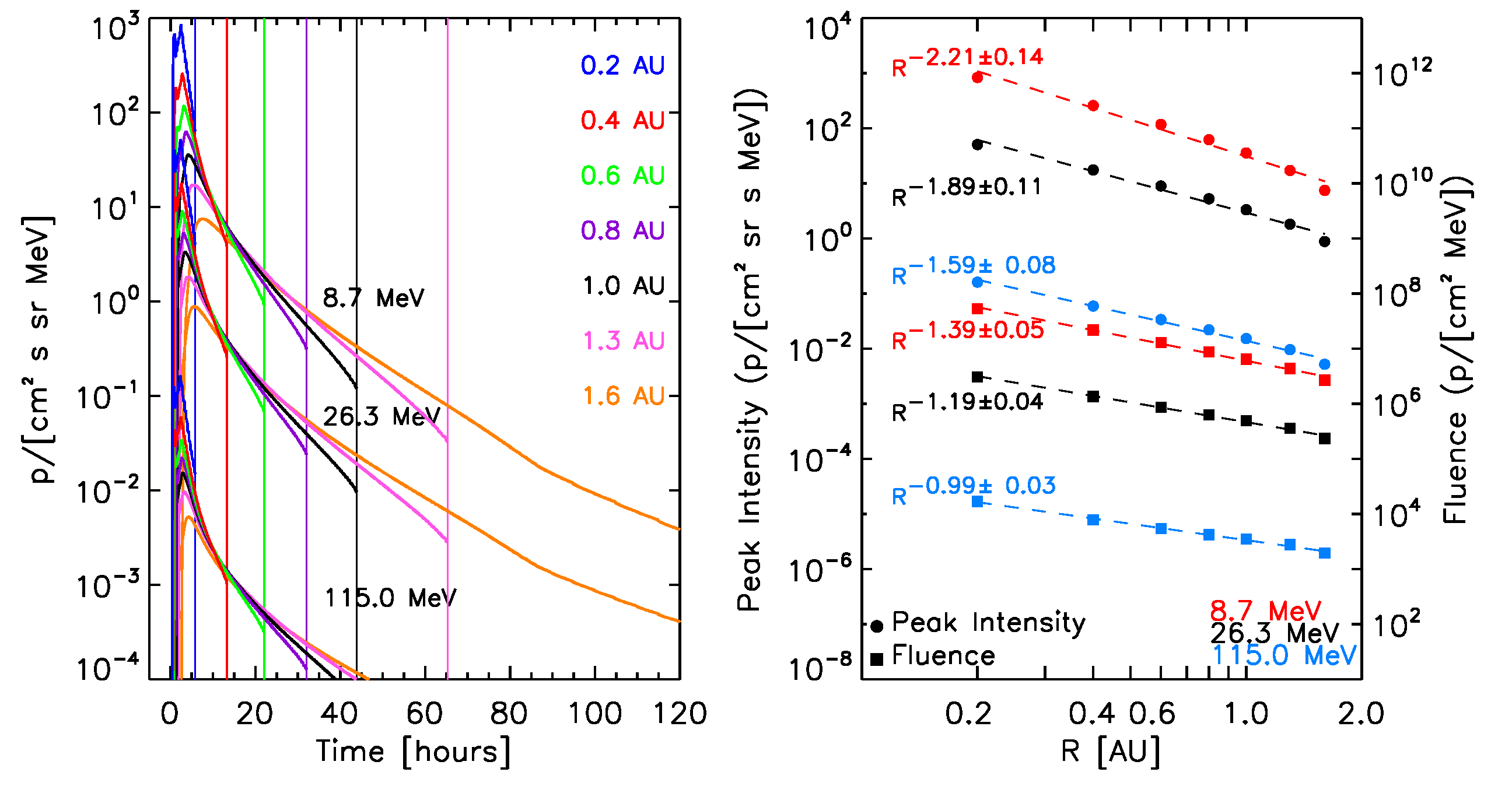 |
June 10, 2000 SEP event: 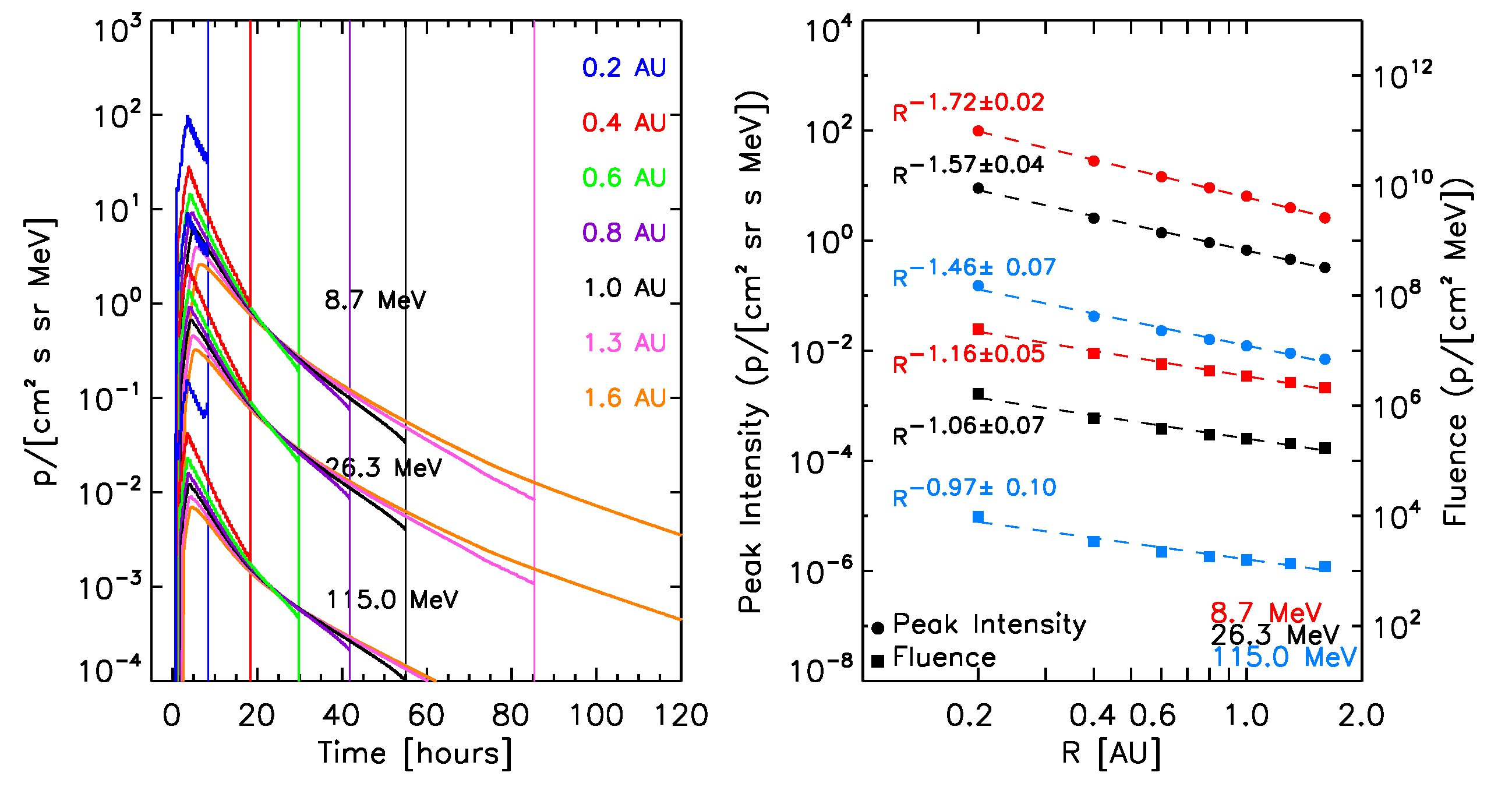 |
April 4, 2000 SEP event: 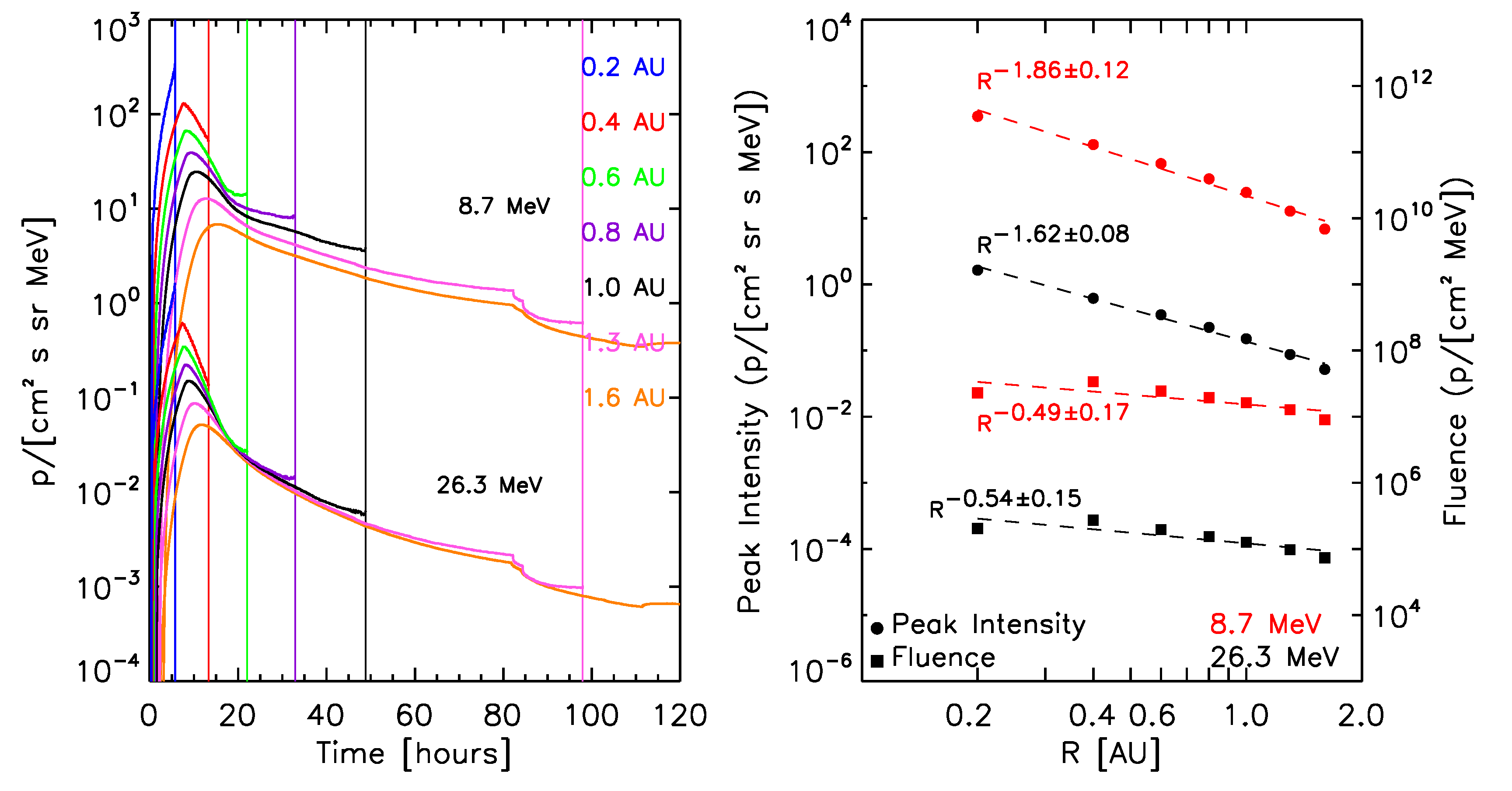 |
|
June 6, 2000 SEP event: 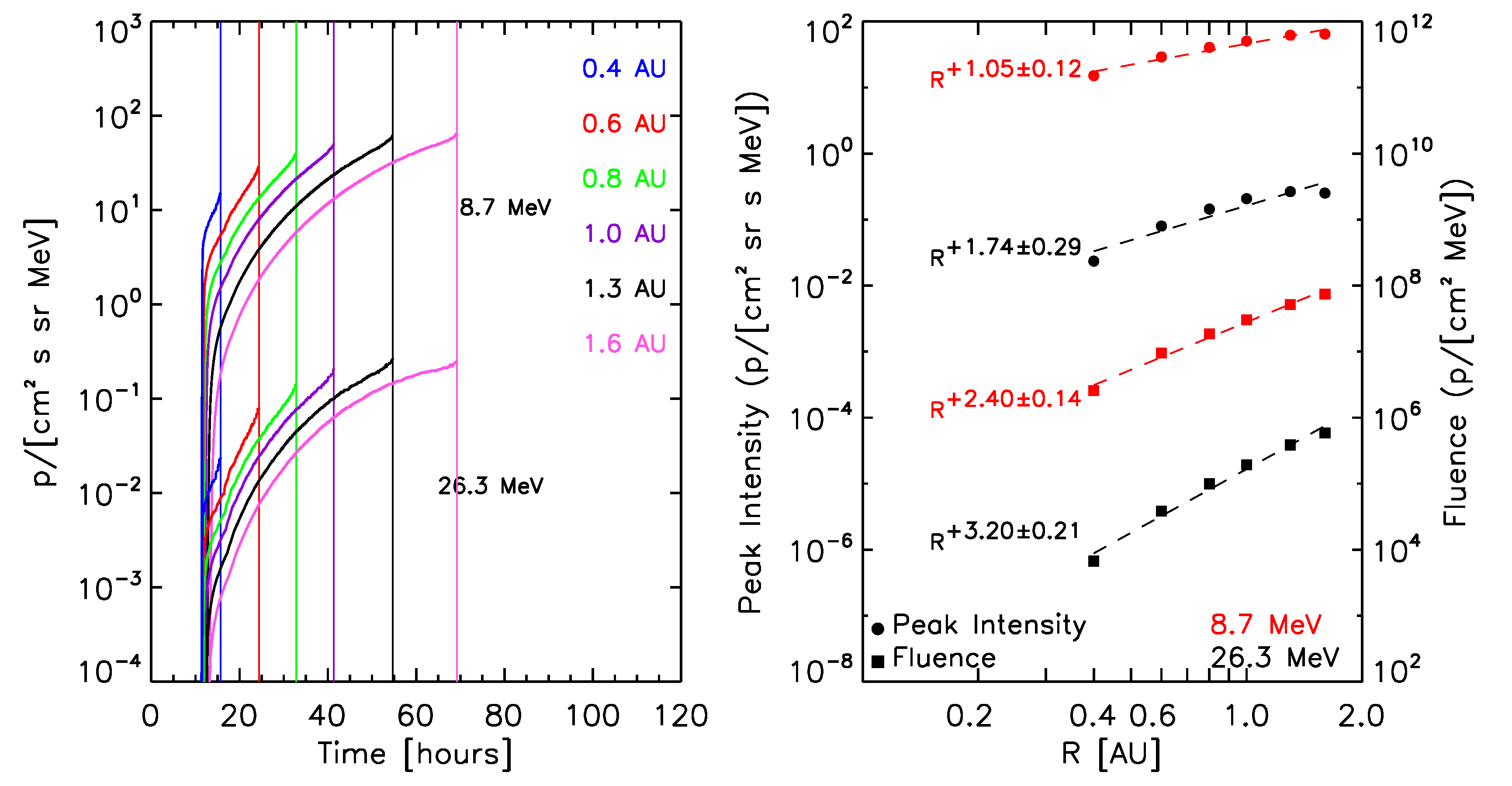 |
March 6, 1989 SEP event: 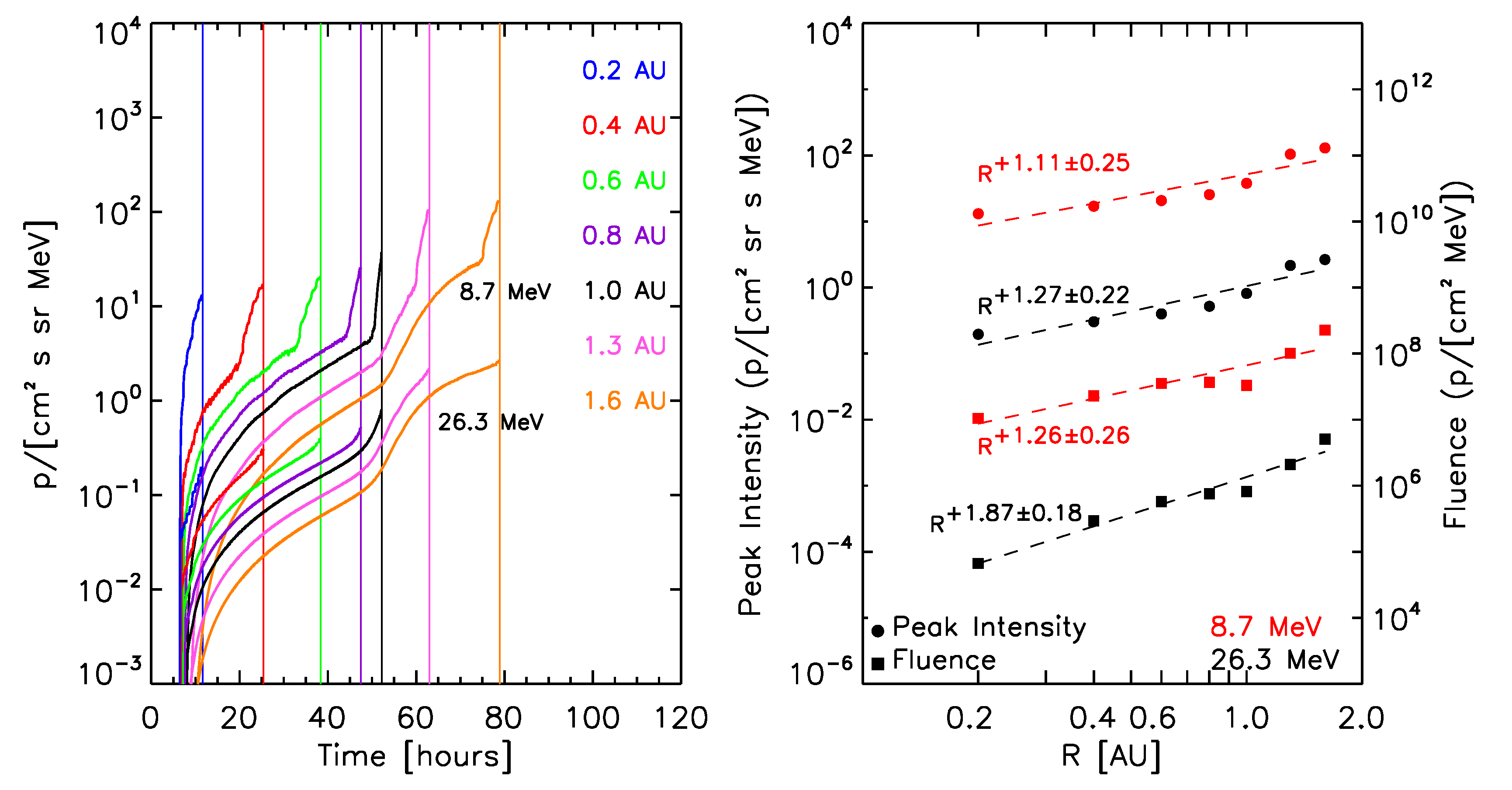 |
March 13, 2012 SEP event: 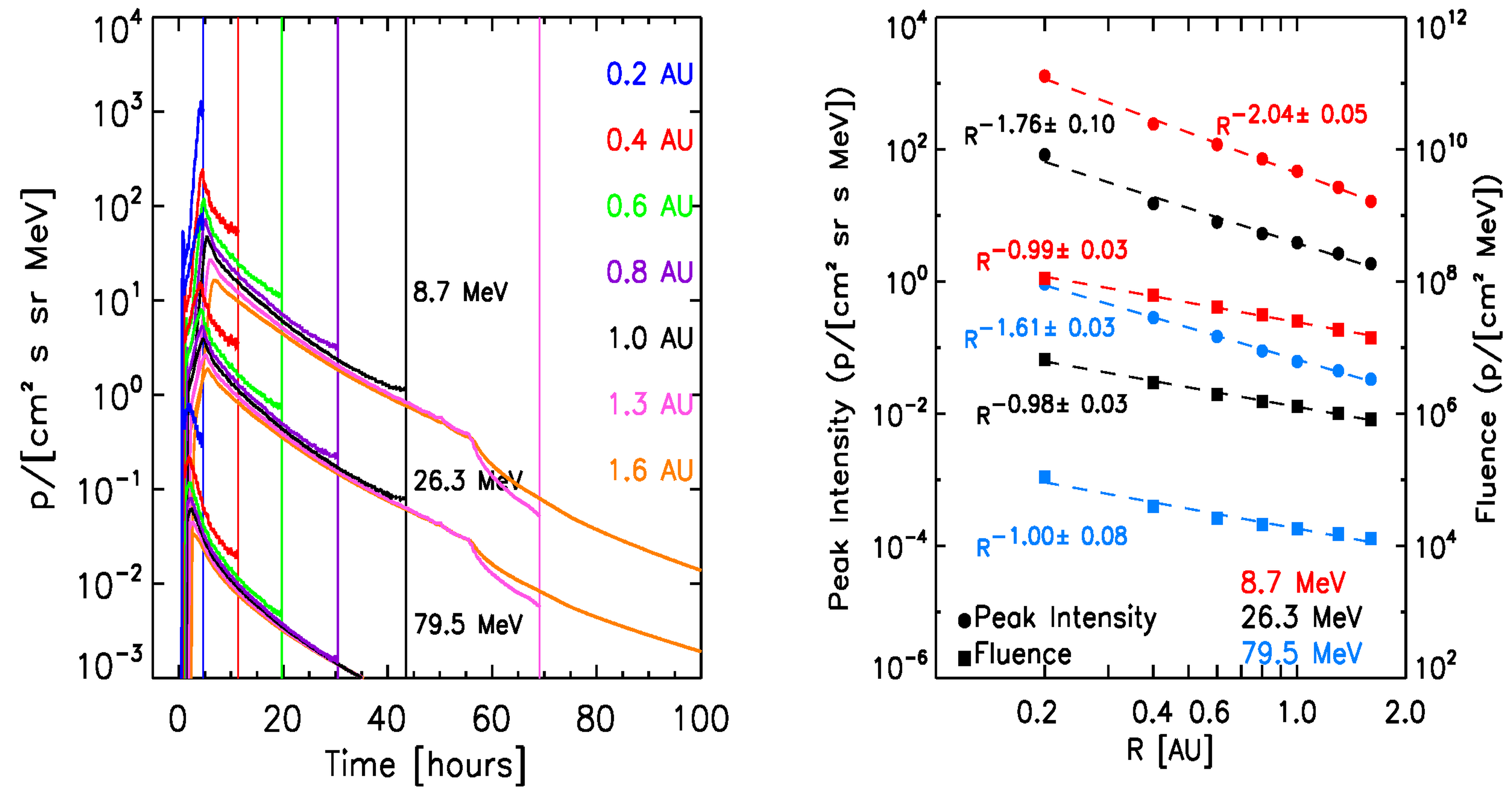 |
|
March 29, 2001 SEP event: 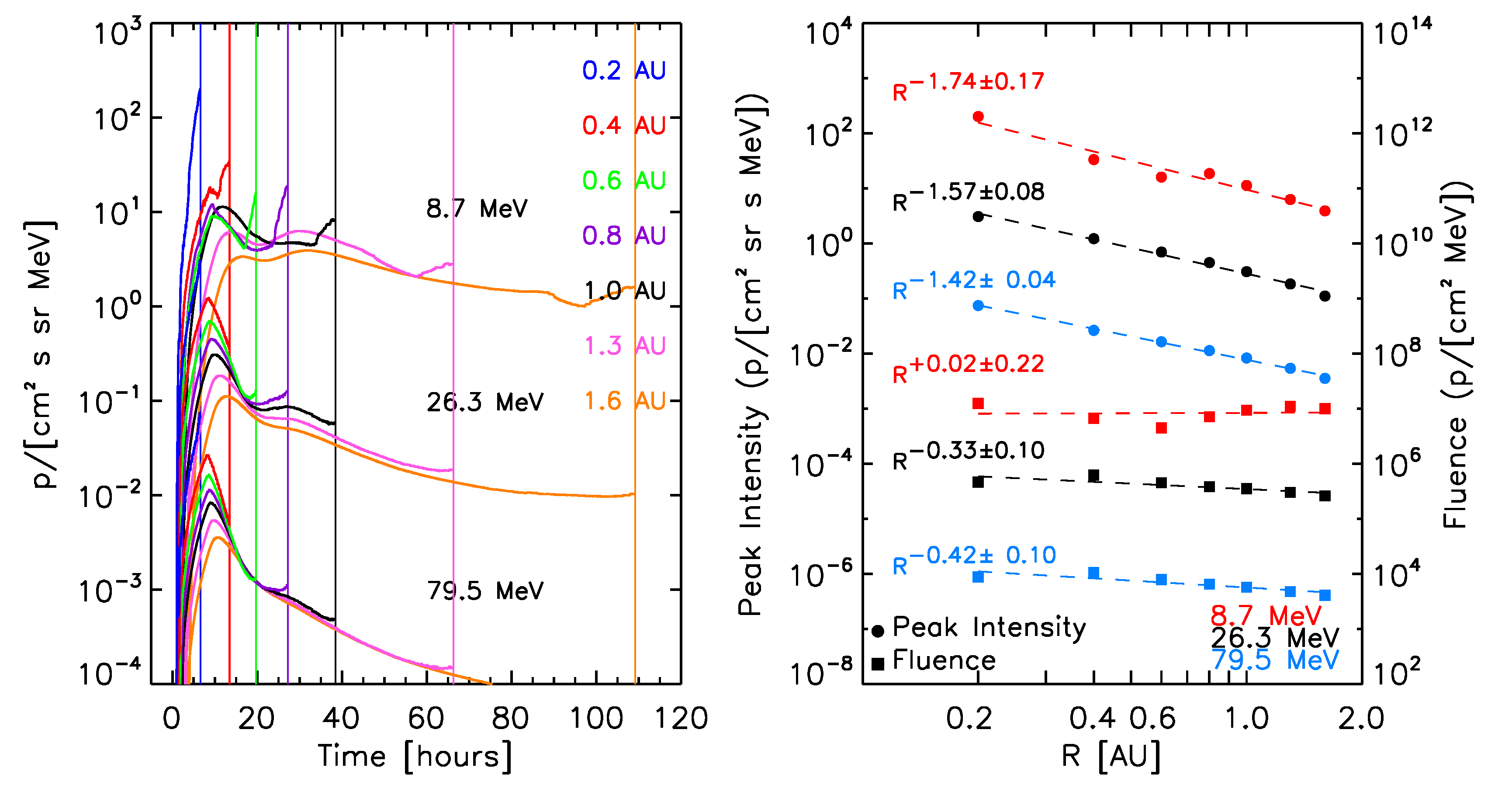 |
September 24, 2001 SEP event: 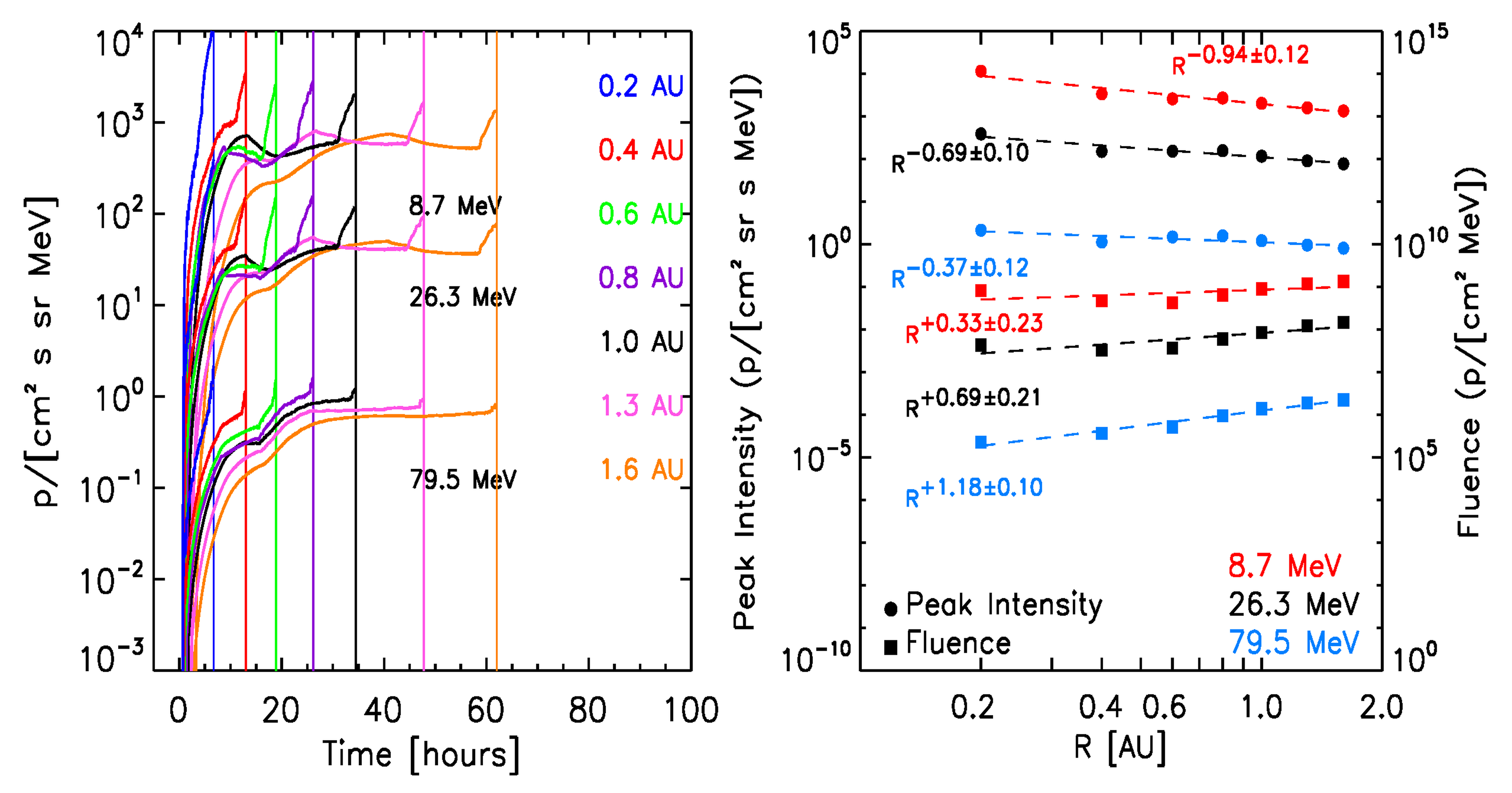 |
October 29, 2003 SEP event: 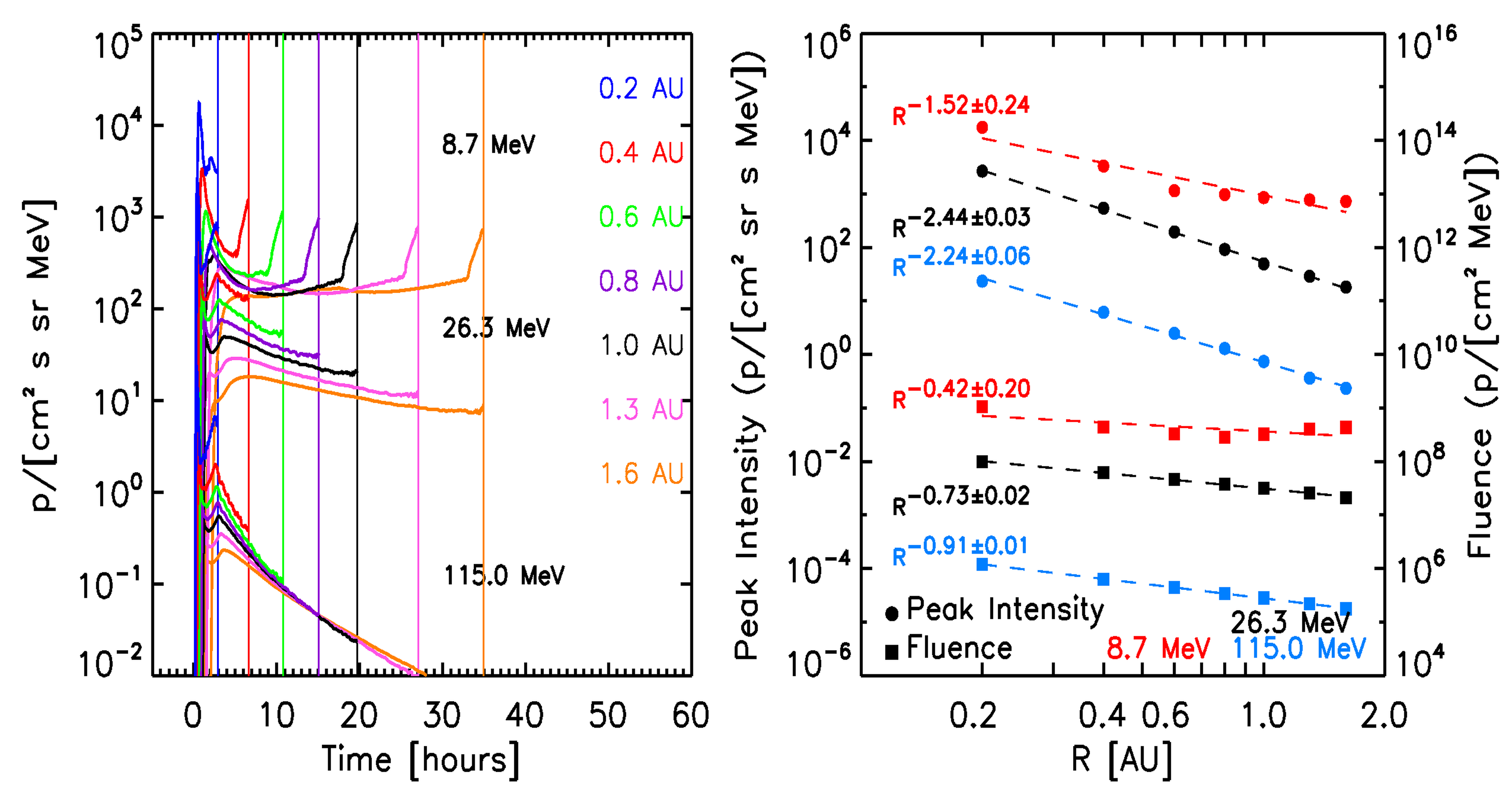 |
|
December 13, 2006 SEP event: 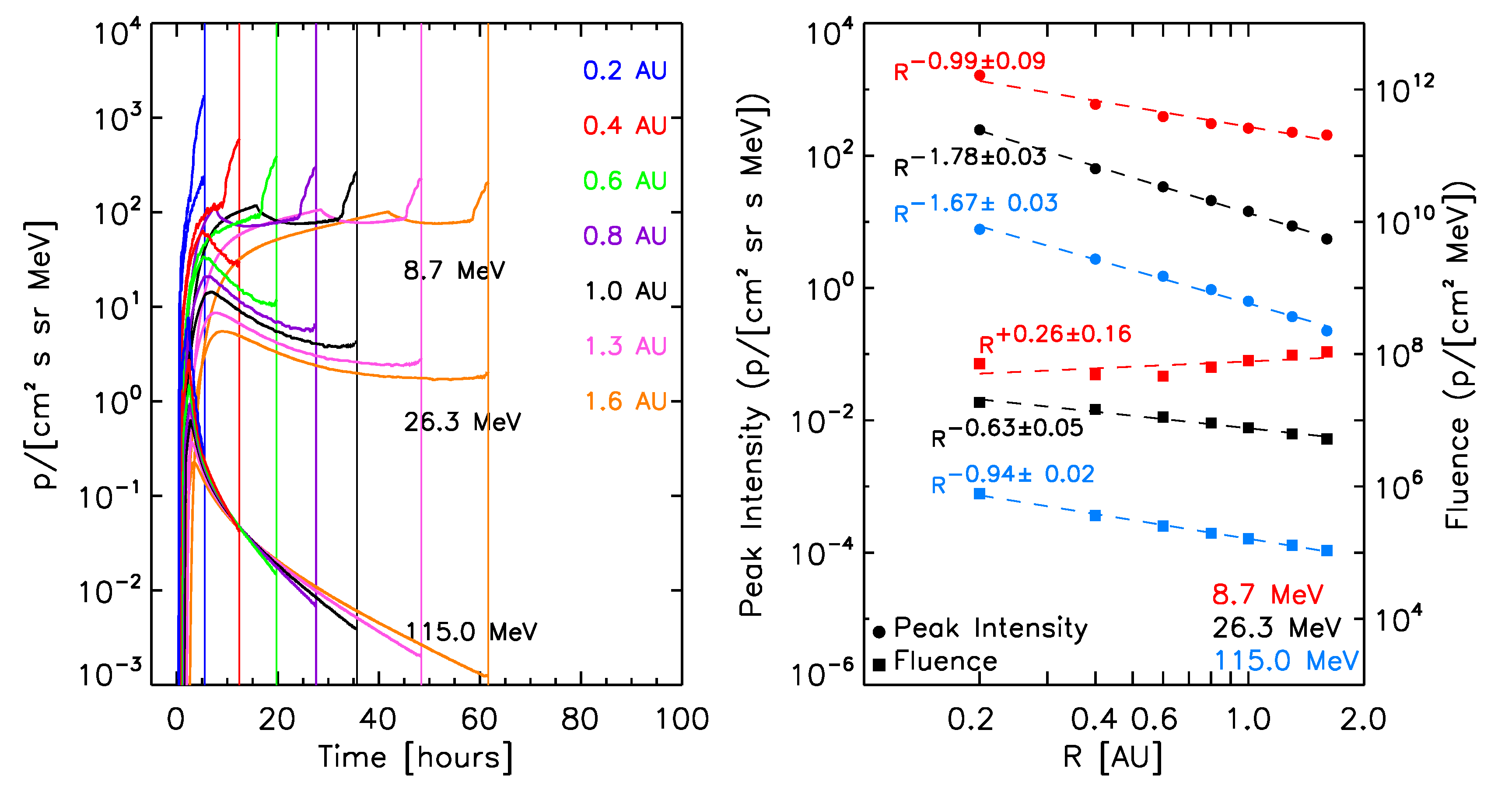 |
The SEP events were classified according to the following characteristics:
From the data the following characteristics were determined:
The SEP events were classified into the following 4 types (10 sub-types):
|
Number of events per event sub-type 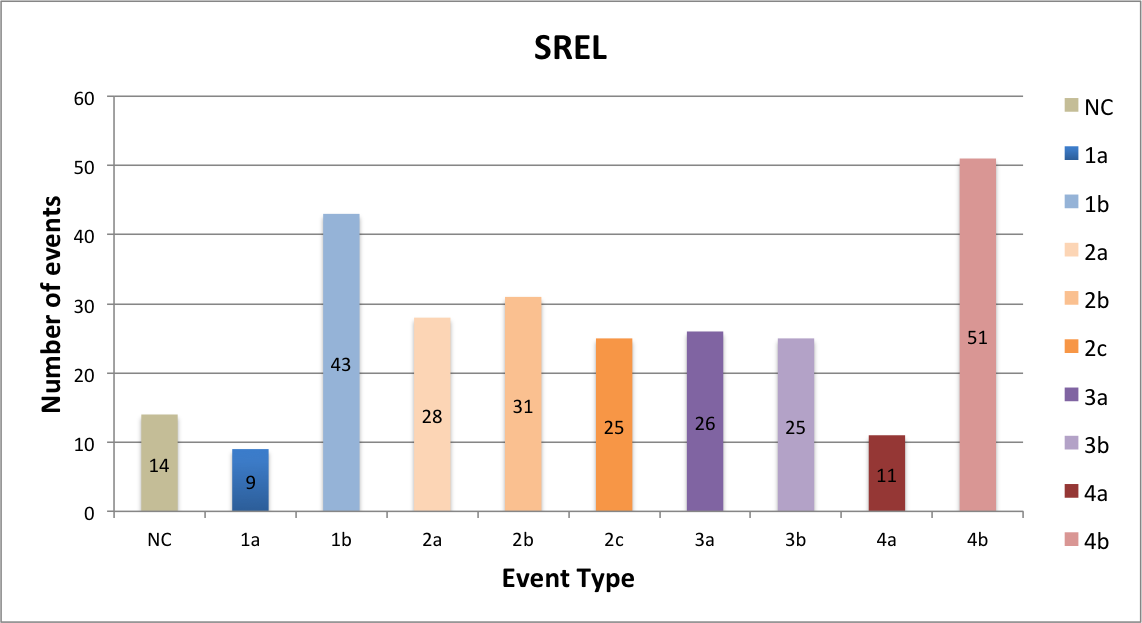 |
|
The main difference with respect to the former classification of the SEP events is that now we have defined a new type, Type 4, consisting of the larger events (in terms of peak intensity and fluence) in SREL. The Type 4 category is constructed from the previous Type 3a. The two Type 4a categories include the eleven events in SREL with the largest peak intensities at both low and high energy. Further, a new category for Type 2 events has been defined with events associated to far eastern solar sources; and the previous Type 3b category has been split into Type 3 a and b according to the heliolongitude of the associated parent source.
SOLPENCO2 provides proton intensity-time profiles for the RDS v2.0 differential channels, from the onset of the particle event up to the shock crossing by 1 AU. In order to estimate the fluence in the post-shock region (i.e., the downstream portion of the particle intensity profiles) we have followed an empirical approach.
We analysed the 35 SEP events in REL, in the period from January 2007 to April 2013, using multi-spacecraft particle observations from the SEPEM RDS v2.0 and from the STEREO spacecraft. For this study, we selected those events showing (i) a clear association with a main solar source, (ii) intensity-time profiles not significantly affected by other local disturbances at 1 AU, and (iii) the pre-shock and post-shock regions of the intensity-time profiles can be clearly identified. The main conclusion is that in the case of events generated by the same solar eruption there is a variation of the downstream-to-total fluence rations (DTFRs) with the heliolongitude of the parent event: the contribution of the fluence of the downstream region to the total fluence of a given SEP event is larger for the eastern instances of the SEP event than for the western ones [22].
Once it was established that there exists a variation of DTFRs with the heliolongitude in SEP events, we extended the study of the DTFR variation with the heliolongitude to:
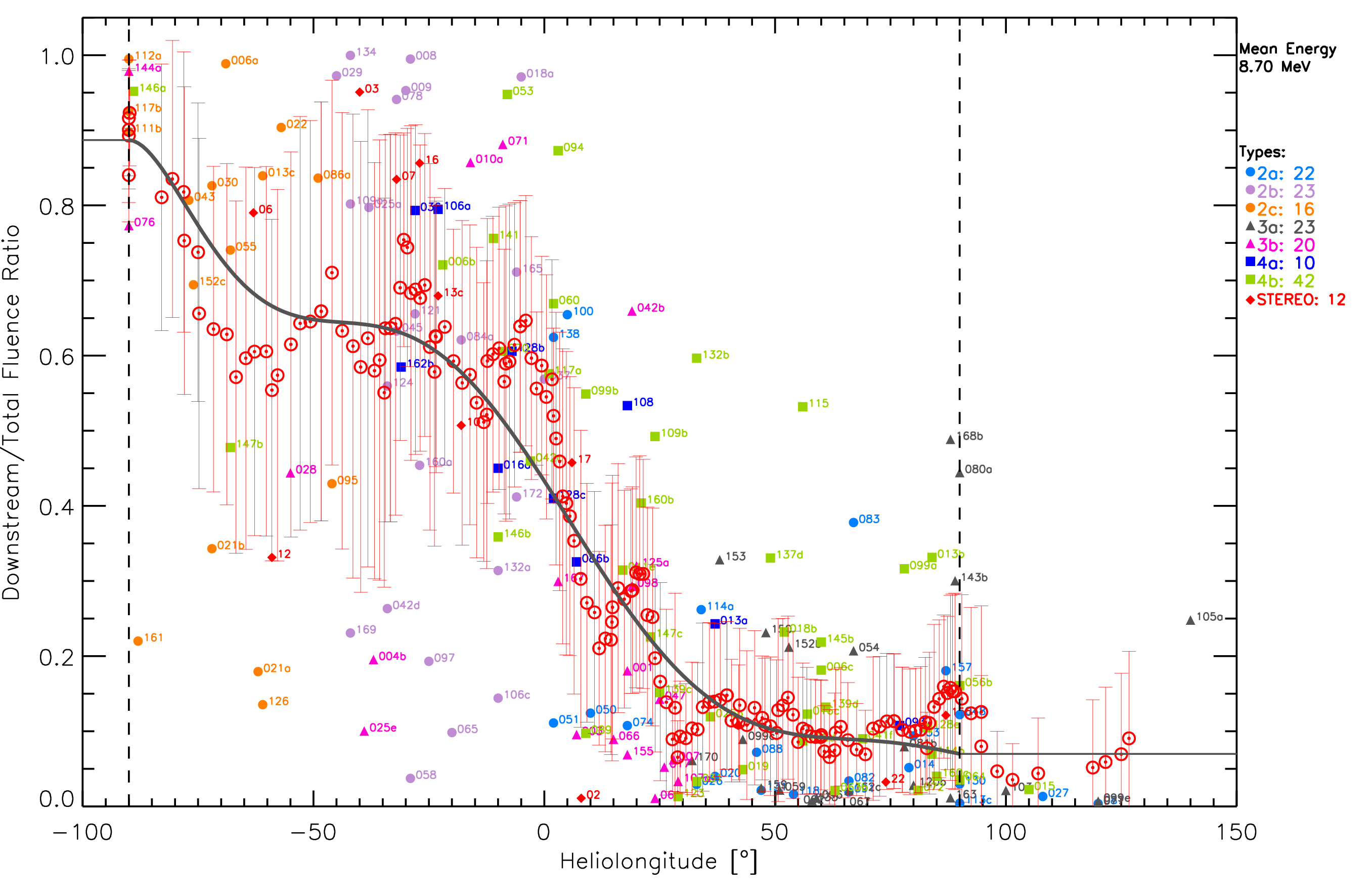 |
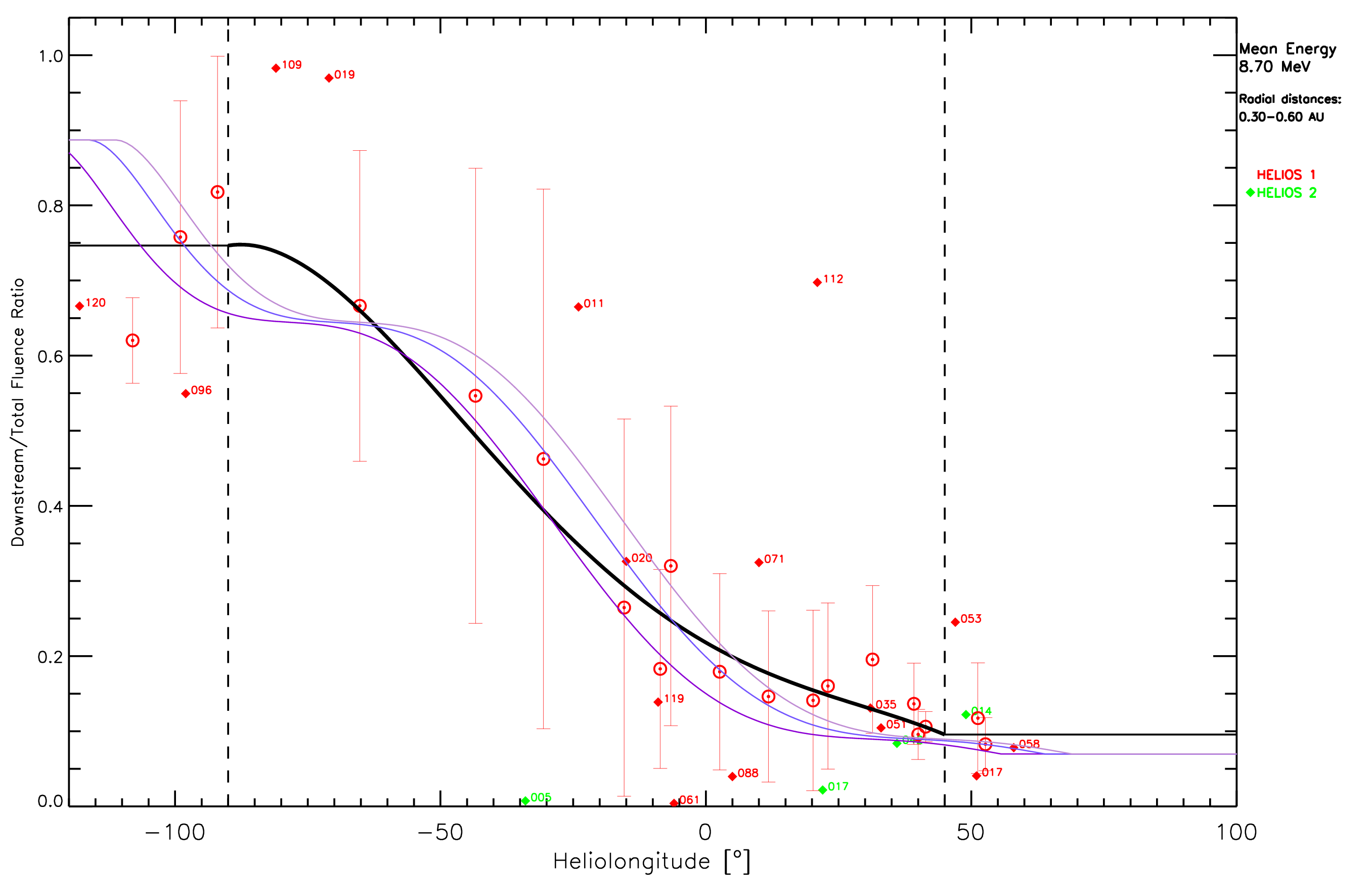 |
|
Type 2c. 1989 March 6 SEP event. 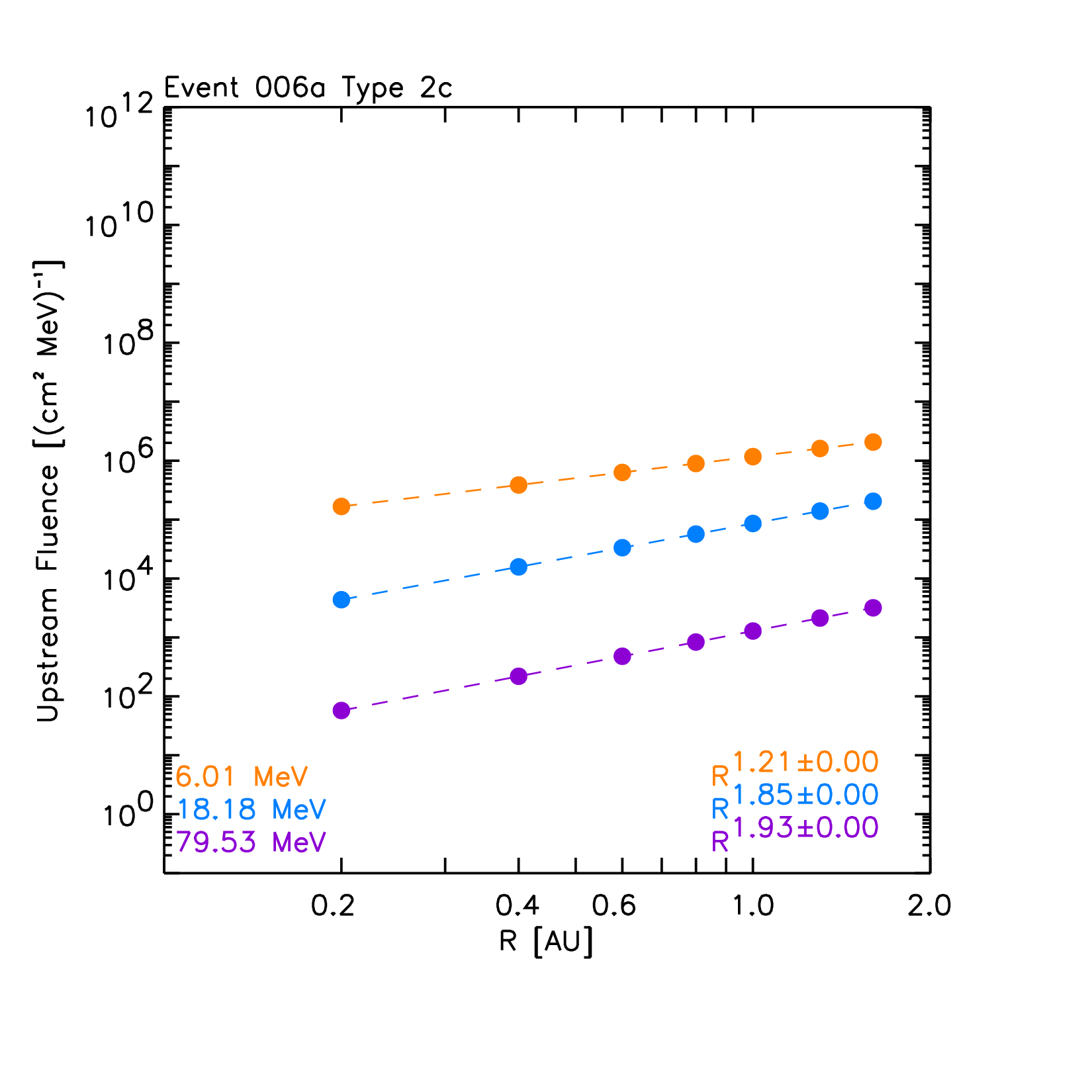
 |
Type 4a-np. 2001 September 24 SEP event. 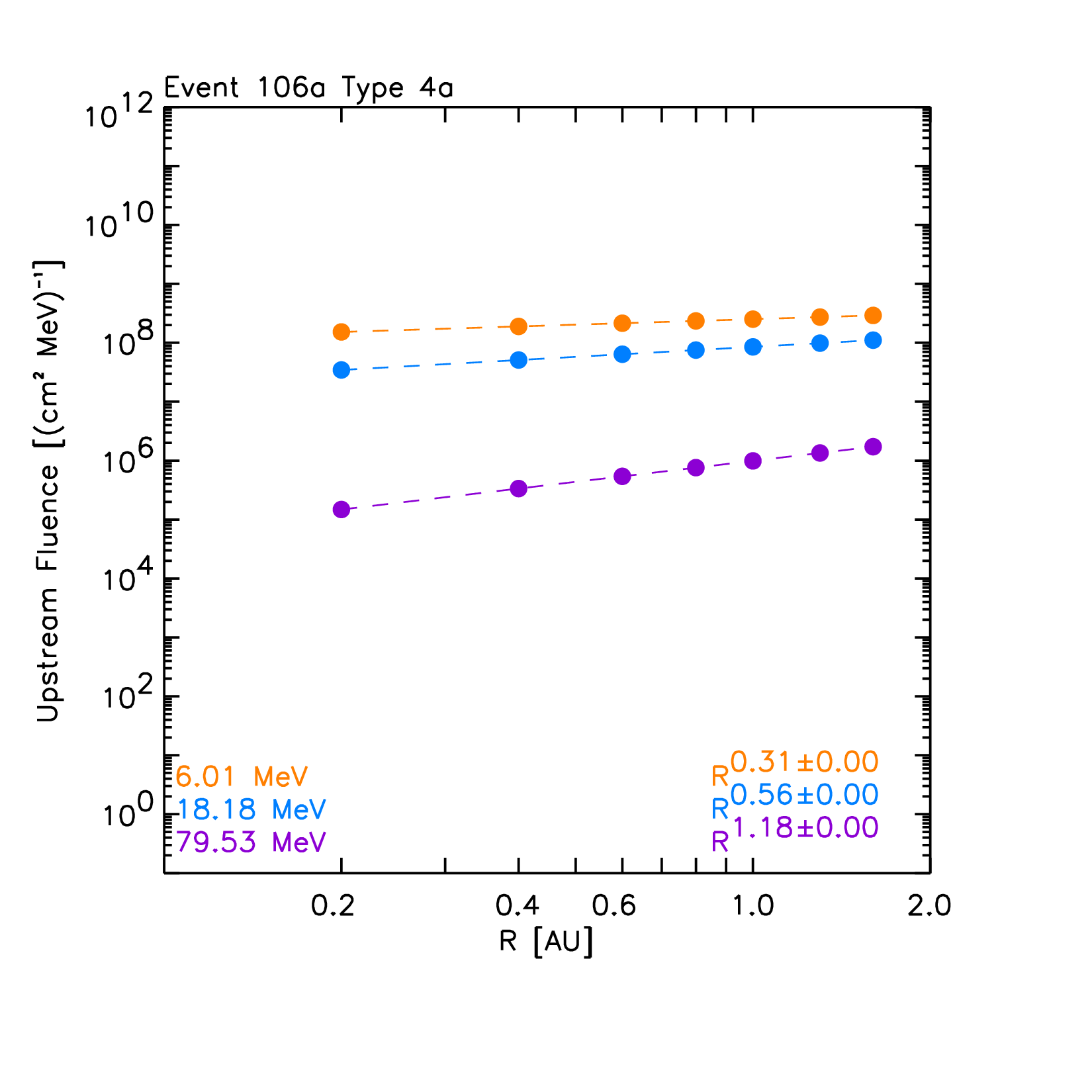
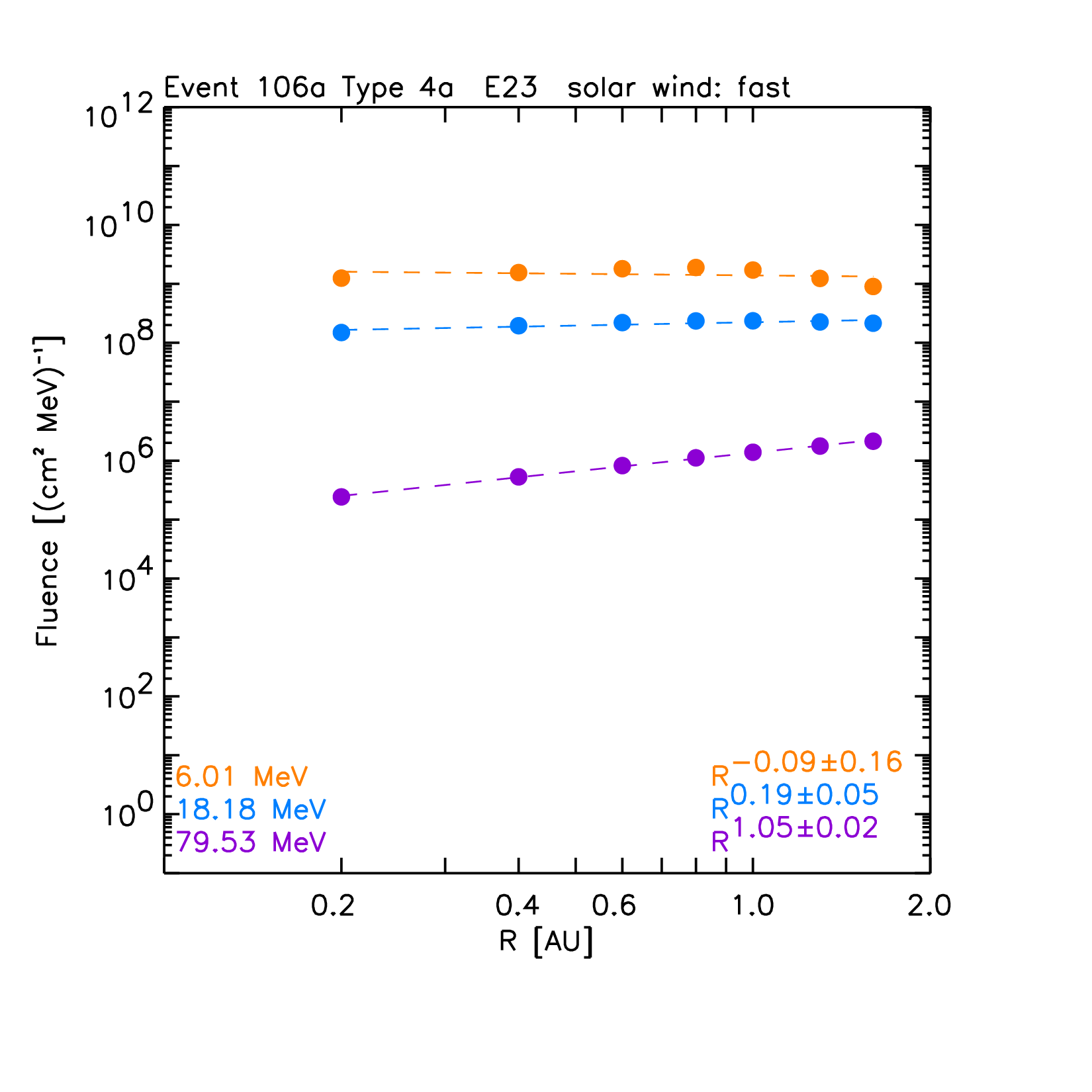 |
Once the SEP events in REL are classified into one of the ten sub-types, the peak intensity and fluence spectra across radial distances can be computed. Figure 13 shows an example of the resulting spectra for the individual SEP event on 13 May 2005. After revision of the data set, this event was classified as a Type 4b event. The left panel of Figure 13 shows the peak intensity energy spectra across the simulated radial distances (colour coded) whereas the right panel shows the corresponding plot for the total fluence. The largest values are obtained for the virtual observer located at 0.2 AU, with the exception of the fluence for the two lower energies. In these latter cases, the predicted heliocentric radial dependence of the fluence is almost flat, resulting from the radial dependence derived by SOLPENCO2 for the 2006 December 13 SEP event (the reference event for Type 4b) for these two energies.
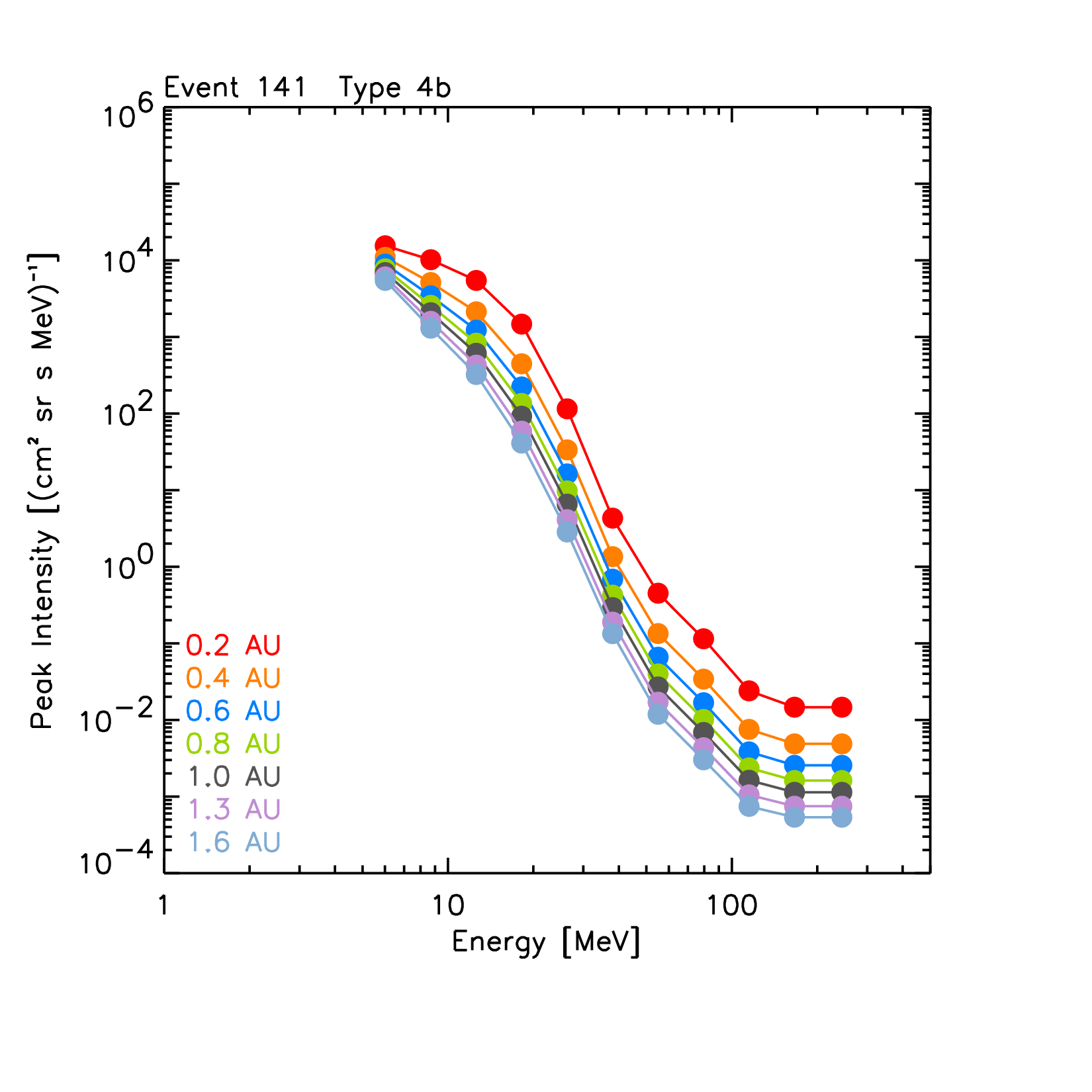
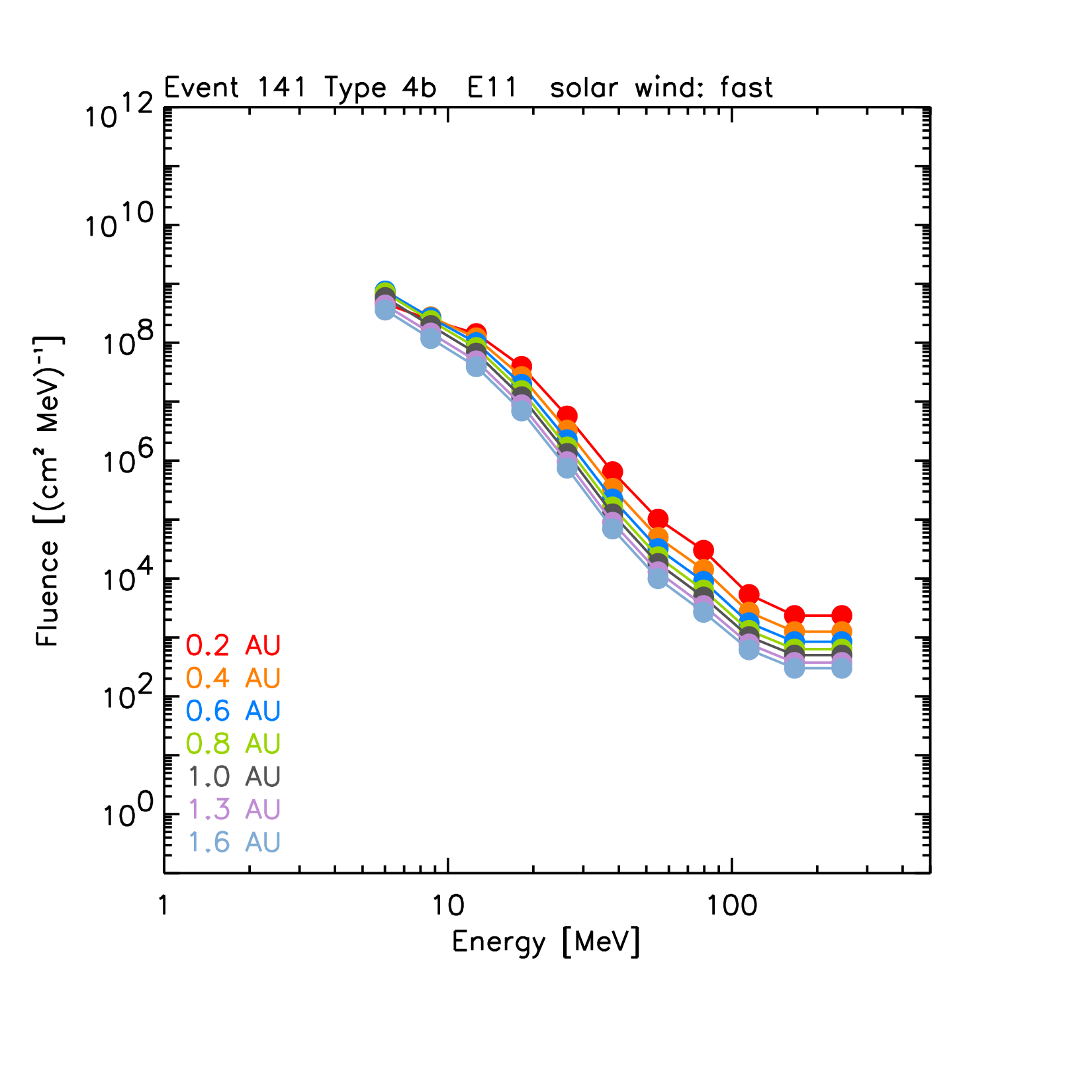 |
| Figure 13. Peak intensity (left) and fluence (right) spectra of the 13 May 2005 SEP event for each modelled radial distance (colour coded as indicated in the legends). SEPEM RDS used is v2.0 with background subtraction described in [22]. |
In compound SEP events, the downstream region of one event is overlapped by the onset of the following event. The contributions of any remaining flux resulting from the first shock or from re-acceleration by the following shock are included in the later event. The method has little background physical support. It is aimed to give an operative input for the statistical model.
In such compound events, the peak intensity of each proton enhancement has been scaled to other radial distances according to its sub-type and the selected value is the highest among the SEP enhancements for each energy and radial distance. To compute the fluences of the compound events, first the fluence of each individual SEP event (or each SEP enhancement) is scaled according to the power law of its sub-type. Next, the scaled fluences are added to account for the fluence of the compound event. Figure 14 shows the example of the Halloween events in October—November 2003. This compound event is formed by 5 SEP events, two of them classified as Type 4a-p and the other three as Type 4b. As in the previous figure, Figure 14 shows the peak intensity (left) and total fluence (right) energy spectra across the simulated radial distances (colour coded) for the Halloween events. For both magnitudes and for all energies, the largest values are predicted for the virtual observer placed at the closest distance from the Sun.
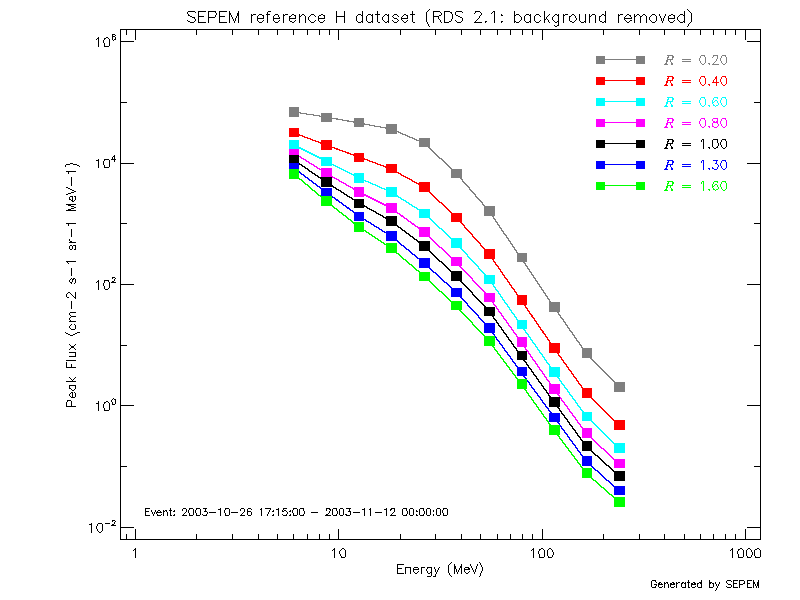
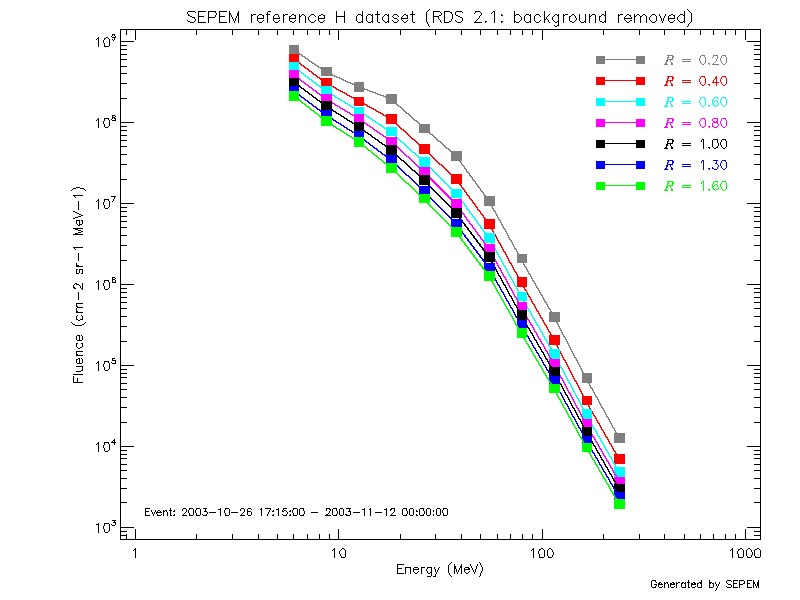 |
| Figure 14. Intensity spectra for the Halloween events (26 October—12 November 2003) using SEPEM RDS v2.1 |
We have presented a methodology (in fact, the first attempt ever) to couple physics-based models, considering the description of gradual SEP events, with statistical SEP environment models, in order to address the variation of the peak intensities and fluence of SEP events for interplanetary missions travelling in the inner heliosphere. The present results may be ameliorated by improving both the SOLPENCO2 tool and the physics-based shock-and-particle (SaP) model described above [8]. In particular, future developments could include (but not only):
The Solar Orbiter and the Parker Solar Probe missions may help to improve and verify our models.
The work presented here is documented in a series of internal ESA/SEPEM Technical Reports. Part of these results is still in the process of publication.
[2] Aran A., B. Sanahuja and D. Lario (2005) Annales Geophysicae 23, 3047.
[3] Aran, A., PhD Thesis, (2007).
[4] Wu, S. T., M. Dryer and S. M. Han (1983) Solar Phys. 84, 395.
[5] Lario D., B. Sanahuja, and A.M. Heras (1998) Astrophys. Journal 509, 415.
[6] Aran A., B. Sanahuja and D. Lario (2008), Advances in Space Research, 42(9), 1492-1499, doi:10.1016/j.asr.2007.08.003
[7] Crosby, N., D. Heynderickx, P. Jiggens et al. (2015), Space Weather, 13, 406-426, doi:10.1002/2013SW001008
[8] Aran, A., C. Jacobs, R. Rodríguez-Gasén et al. (2011). WP410: Initial and boundary conditions for the shock-and- particle model. SEPEM Technical Report, ESA/ESTEC Contract 20162/06/NL/JD, 1–58.
[9] Pomoell, J., A. Aran, C. Jacobs et al. (2015) , Journal of Space Weather and Space Climate, 5, A12, doi:10.1051/swsc/201505.
[10] Jiggens. P., S. Gabriel, D. Heynderickx, et al. (2012), IEEE Trans. Nuc. Sci., 59(4), 1066.
[11] Sandberg, I., (2014), SEPCALIB Final Report, 1-40.
[12] Cane H.V. and D. Lario, (2006), Space Science Reviews, 123, 45-56.
[13] Jacobs C. and S. Poedts (2011), Advances in Space Research, 48, 1958.
[14] A. M. Heras, B. Sanahuja, Z. Smith et al. (1992), Astrophys. Journal 391, 359
[15] A.M. Heras, B. Sanahuja, D. Lario et al. (1995), Astrophys. Journal 445, 497.
[16] E. C. Roelof (1969), in Lectures in High Energy Astrophysics, NASA SP-199, ed. H. Ögelman & J. R. Wayland, 111.
[17] D. Ruffolo (1995), Astrophys. Journal, 442, 861.
[18] J. R. Jokipii (1966) Astrophys. Journal 146, 480.
[19] A. Aran et al. (2007) Astron. & Astrophys. 469, 1123.
[20] D. Lario, M.-B. Kallenrode, et al (2006) Astrophys. Journal 653, 1531
[21] D. Lario, A. Aran et al. (2007) Advances in Space Research 40, 289.
[22] Pacheco, D., A. Aran, N. Agueda, B. Sanahuja (2017), SOL2UP WP1200: Evaluation of the downstream contribution to total fluence, SOL2UP Technical Report TN-1, ESA/ESTEC contract 4000114116/15/NL/HK, 1—134 (2017); Pacheco et al., JSWSC in preparation (2017).
[23] Lario, D., A. Aran, R. Gómez-Herrero, et al. (2013), Astrophys. J., 767, 41.